Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
On the theory of the recombination of ions in gases at high pressures
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 2 / April 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 219-233
- Print publication:
- April 1932
-
- Article
- Export citation
On some series of functions, (3)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 2 / April 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 190-205
- Print publication:
- April 1932
-
- Article
- Export citation
Photo-electric absorption in hydrogen-like atoms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 2 / April 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 209-218
- Print publication:
- April 1932
-
- Article
- Export citation
PSP volume 28 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- January 1932
-
- Article
-
- You have access
- Export citation
The upper limit of energy in the β-ray spectrum of thorium C″
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 115-120
- Print publication:
- January 1932
-
- Article
- Export citation
PSP volume 28 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- January 1932
-
- Article
-
- You have access
- Export citation
Explicit formulae connecting Hölder's, Cesàro's and another mean value
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-17
- Print publication:
- January 1932
-
- Article
- Export citation
On the determination of the horizontal component of the earth's magnetic field by a coupled oscillations method
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 109-114
- Print publication:
- January 1932
-
- Article
- Export citation
The ‘relaxation’ term in Debye and Hückel's theory of ionic mobility
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 83-92
- Print publication:
- January 1932
-
- Article
- Export citation
An attempt to detect the spontaneous transformation of helium into penetrating radiation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 124-127
- Print publication:
- January 1932
-
- Article
- Export citation
A quantum mechanical theory of energy exchanges between inert gas atoms and a solid surface
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 136-164
- Print publication:
- January 1932
-
- Article
- Export citation
The interval between the departure of the disintegration particle and the emission of the gamma radiation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 128-135
- Print publication:
- January 1932
-
- Article
- Export citation
The general surfaces in four dimensions with one or two apparent triple points
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 51-54
- Print publication:
- January 1932
-
- Article
- Export citation
Note on the instability of a surface of discontinuity
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 35-44
- Print publication:
- January 1932
-
- Article
- Export citation
Note on a high-tension supply for Geiger counters operated from A.C. mains
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 121-123
- Print publication:
- January 1932
-
- Article
- Export citation
Note in regard to surfaces in space of four dimensions, in particular rational surfaces*
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 62-82
- Print publication:
- January 1932
-
- Article
- Export citation
The tangent planes to a degenerate surface
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 45-50
- Print publication:
- January 1932
-
- Article
- Export citation
The collision of electrons with rotating dipoles
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 99-105
- Print publication:
- January 1932
-
- Article
- Export citation
Note on a new power-angle diagram for alternators
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 106-108
- Print publication:
- January 1932
-
- Article
- Export citation
The application of quadratic forms in an infinity of variables to boundary problems in partial differential equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 1 / January 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 23-34
- Print publication:
- January 1932
-
- Article
- Export citation
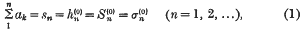
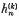 are defined by
are defined by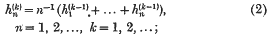
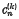 are defined by
are defined by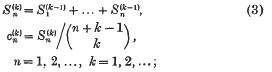
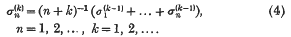
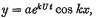
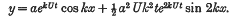
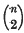 double lines, and in threes, forming
double lines, and in threes, forming 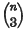 triple points. The tangent cone to φ from an arbitrary point consists of
triple points. The tangent cone to φ from an arbitrary point consists of 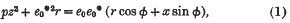
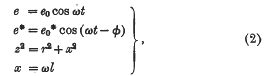
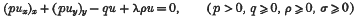
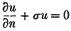 on Γ, the boundary of
on Γ, the boundary of 