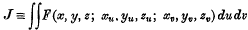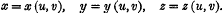Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
Some chains of theorems derived by successive projection
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 45-51
- Print publication:
- January 1933
-
- Article
- Export citation
The equilibrium of atoms and ions adsorbed on a metal surface
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 161-164
- Print publication:
- January 1933
-
- Article
- Export citation
Configurations defined by six lines in space of three dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 52-68
- Print publication:
- January 1933
-
- Article
- Export citation
The upper limit of energy in the β-ray spectrum of actinium B
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 156-160
- Print publication:
- January 1933
-
- Article
- Export citation
The reflexion of light at a surface covered by a monomolecular film
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 116-130
- Print publication:
- January 1933
-
- Article
- Export citation
On the prior probability in the theory of sampling
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 83-87
- Print publication:
- January 1933
-
- Article
- Export citation
PSP volume 29 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- January 1933
-
- Article
-
- You have access
- Export citation
Rational normal octavic surfaces with a double line, in space of five dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 95-102
- Print publication:
- January 1933
-
- Article
- Export citation
PSP volume 29 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- January 1933
-
- Article
-
- You have access
- Export citation
Degenerate surfaces in higher space
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 88-94
- Print publication:
- January 1933
-
- Article
- Export citation
The spectrum of the self-adjoint partial differential equation in any domain
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 23-44
- Print publication:
- January 1933
-
- Article
- Export citation
Some comments on the relation between ionisation and ionisation current in gases at high pressures
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 149-155
- Print publication:
- January 1933
-
- Article
- Export citation
The sum of powers as canonical expression
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 69-82
- Print publication:
- January 1933
-
- Article
- Export citation
Some observations on the theory of interchange of vibrational and translational energy
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 136-141
- Print publication:
- January 1933
-
- Article
- Export citation
Three related quartic curves in four dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 4 / October 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 403-415
- Print publication:
- October 1932
-
- Article
- Export citation
Some factors in the design of hot cathode X-ray tubes for steady running
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 4 / October 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 497-508
- Print publication:
- October 1932
-
- Article
- Export citation
The emission of positive ions from hot tungsten
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 4 / October 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 490-496
- Print publication:
- October 1932
-
- Article
- Export citation
Extension of a theorem of C. G. F. James
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 4 / October 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 421-426
- Print publication:
- October 1932
-
- Article
- Export citation
On double integrals in the calculus of variations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 4 / October 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 442-454
- Print publication:
- October 1932
-
- Article
- Export citation
Additional note on plane congruences and fifth incidence theorems
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 4 / October 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 416-420
- Print publication:
- October 1932
-
- Article
- Export citation
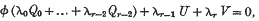
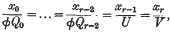
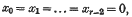

 or similar, these conditions becoming identical at any part of the boundary of
or similar, these conditions becoming identical at any part of the boundary of 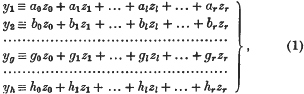

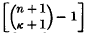 ; the representation is effected by taking as independent homogeneous coordinates of a [
; the representation is effected by taking as independent homogeneous coordinates of a [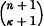 determinants of order
determinants of order