Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
On surfaces of sectional genus four
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 184-194
- Print publication:
- May 1933
-
- Article
- Export citation
The generalised product moment distribution in a normal system
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 260-270
- Print publication:
- May 1933
-
- Article
- Export citation
An integral which occurs in statistics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 271-276
- Print publication:
- May 1933
-
- Article
- Export citation
The effect of a magnetic field on relative gravity determinations with invar pendulums
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 288-296
- Print publication:
- May 1933
-
- Article
- Export citation
Incidence scrolls
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 235-244
- Print publication:
- May 1933
-
- Article
- Export citation
Slow rotation of a circular cylinder in a viscous fluid bounded by parallel walls
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 277-287
- Print publication:
- May 1933
-
- Article
- Export citation
A theorem on transitive groups
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 257-259
- Print publication:
- May 1933
-
- Article
- Export citation
A study of the intensity variations of downcoming wireless waves
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 301-318
- Print publication:
- May 1933
-
- Article
- Export citation
PSP volume 29 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- May 1933
-
- Article
-
- You have access
- Export citation
An extension of Morley's chain of theorems on circles*
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 165-172
- Print publication:
- May 1933
-
- Article
- Export citation
The reflection of electrons from standing light waves
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 297-300
- Print publication:
- May 1933
-
- Article
- Export citation
Some surfaces containing triple curves, II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 178-183
- Print publication:
- May 1933
-
- Article
- Export citation
Isolated singular points in the theory of algebraic surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 212-230
- Print publication:
- May 1933
-
- Article
- Export citation
On the product of two Legendre polynomials
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 173-177
- Print publication:
- May 1933
-
- Article
- Export citation
The sums of powers as simultaneous canonical expressions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 245-256
- Print publication:
- May 1933
-
- Article
- Export citation
PSP volume 29 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- May 1933
-
- Article
-
- You have access
- Export citation
The densities of the regular polytopes, Part 3*
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-22
- Print publication:
- January 1933
-
- Article
- Export citation
Planar threefolds in space of four dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 103-115
- Print publication:
- January 1933
-
- Article
- Export citation
Surface motion of sputtered particles
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 131-135
- Print publication:
- January 1933
-
- Article
- Export citation
Asymptotic expansions of the expressions for the partition function and the rotational specific heat of a rigid polyatomic molecule for high temperatures
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 1 / January 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 142-148
- Print publication:
- January 1933
-
- Article
- Export citation
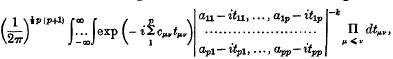
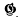 be any transitive permutation group on the
be any transitive permutation group on the 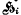 be the subgroup of
be the subgroup of 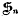 on 1, …,
on 1, …, 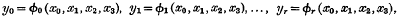
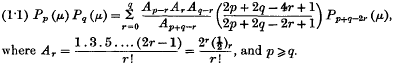
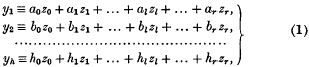
 triple points.
triple points.

