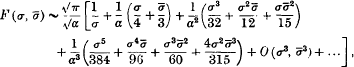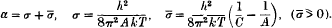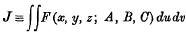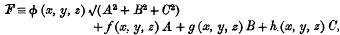Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
The algebraic surfaces contained by a cubic primal in four dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 4 / 30 October 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 484-486
- Print publication:
- 30 October 1933
-
- Article
- Export citation
PSP volume 29 issue 4 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 4 / 30 October 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b10
- Print publication:
- 30 October 1933
-
- Article
-
- You have access
- Export citation
Non-continuous interaction between hosts and parasites
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 4 / 30 October 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 487-491
- Print publication:
- 30 October 1933
-
- Article
- Export citation
Homogeneous variables in classical dynamics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 3 / 30 July 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 389-400
- Print publication:
- 30 July 1933
-
- Article
- Export citation
PSP volume 29 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 3 / 30 July 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- 30 July 1933
-
- Article
-
- You have access
- Export citation
The exact difference equation of the first order
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 3 / 30 July 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 373-381
- Print publication:
- 30 July 1933
-
- Article
- Export citation
On the transformation of certain singular surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 3 / 30 July 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 319-330
- Print publication:
- 30 July 1933
-
- Article
- Export citation
Bisecant curves of ruled surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 3 / 30 July 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 382-388
- Print publication:
- 30 July 1933
-
- Article
- Export citation
The deflection of a cantilever bar rotated under end load
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 3 / 30 July 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 423-439
- Print publication:
- 30 July 1933
-
- Article
- Export citation
Rational normal octavic surfaces with a double line, in space of five dimensions: Addition
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 3 / 30 July 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 405-406
- Print publication:
- 30 July 1933
-
- Article
- Export citation
Diagonal matrices
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 3 / 30 July 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 347-372
- Print publication:
- 30 July 1933
-
- Article
- Export citation
The rotational specific heat of a polyatomic molecule for high temperatures—correction
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 3 / 30 July 1933
- Published online by Cambridge University Press:
- 24 October 2008, p. 407
- Print publication:
- 30 July 1933
-
- Article
- Export citation
A constant deviation X-ray vacuum monochromator
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 3 / 30 July 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 408-416
- Print publication:
- 30 July 1933
-
- Article
- Export citation
Note on thermal instability in cylindrical condensers due to dielectric losses
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 3 / 30 July 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 401-404
- Print publication:
- 30 July 1933
-
- Article
- Export citation
A representation of [k]'s of [m] by points of [(m − k) (k + 1)]
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 3 / 30 July 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 331-346
- Print publication:
- 30 July 1933
-
- Article
- Export citation
PSP volume 29 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 3 / 30 July 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- 30 July 1933
-
- Article
-
- You have access
- Export citation
An experiment on dispersion
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 3 / 30 July 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 417-422
- Print publication:
- 30 July 1933
-
- Article
- Export citation
The general double integral problem in the calculus of variations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 207-211
- Print publication:
- May 1933
-
- Article
- Export citation
On Gauss's proof of the normal law of errors
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 231-234
- Print publication:
- May 1933
-
- Article
- Export citation
Related quadrics and systems of a rational quartic curve
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 29 / Issue 2 / May 1933
- Published online by Cambridge University Press:
- 24 October 2008, pp. 195-206
- Print publication:
- May 1933
-
- Article
- Export citation
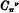 is a bisecant curve of order
is a bisecant curve of order 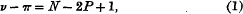
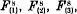 , and
, and 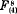 representable on a plane respectively by the systems of curves
representable on a plane respectively by the systems of curves 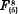 represented by the plane system
represented by the plane system