Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
On the probability of artificial nuclear transformations and its connection with the vector model of the nucleus
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 4 / October 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 561-566
- Print publication:
- October 1934
-
- Article
- Export citation
On the regularity of surfaces, II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 3 / July 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 271-286
- Print publication:
- July 1934
-
- Article
- Export citation
The heat of adsorption of hydrogen on tungsten
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 3 / July 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 376-379
- Print publication:
- July 1934
-
- Article
- Export citation
On the annihilation radiation of the positron
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 3 / July 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 347-354
- Print publication:
- July 1934
-
- Article
- Export citation
PSP volume 30 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 3 / July 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- July 1934
-
- Article
-
- You have access
- Export citation
The flow due to a rotating disc
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 3 / July 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 365-375
- Print publication:
- July 1934
-
- Article
- Export citation
Foucault currents in cylindrical shells and ribbons
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 3 / July 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 341-346
- Print publication:
- July 1934
-
- Article
- Export citation
A theorem on Newton's polygon
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 3 / July 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 287-296
- Print publication:
- July 1934
-
- Article
- Export citation
Evidence for a new type of disintegration produced by neutrons
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 3 / July 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 357-364
- Print publication:
- July 1934
-
- Article
- Export citation
Potential functions with periodicity in one coordinate
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 3 / July 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 315-326
- Print publication:
- July 1934
-
- Article
- Export citation
A hydrogen discharge tube for spectrographic work
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 3 / July 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 355-356
- Print publication:
- July 1934
-
- Article
- Export citation
The vector representation of a sample
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 3 / July 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 327-340
- Print publication:
- July 1934
-
- Article
- Export citation
Multiple canonical surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 3 / July 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 297-308
- Print publication:
- July 1934
-
- Article
- Export citation
On the ambiguity in the specification of a two-sheeted surface by its branch curve
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 3 / July 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 309-314
- Print publication:
- July 1934
-
- Article
- Export citation
PSP volume 30 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 3 / July 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- July 1934
-
- Article
-
- You have access
- Export citation
The distribution of quadratic forms in a normal system, with applications to the analysis of covariance
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 178-191
- Print publication:
- 30 April 1934
-
- Article
- Export citation
On surfaces of sectional genus five
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 123-133
- Print publication:
- 30 April 1934
-
- Article
- Export citation
Investigations on condensation phenomena in mercury vapour
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 216-224
- Print publication:
- 30 April 1934
-
- Article
- Export citation
Discussion of the infinite distribution of electrons in the theory of the positron
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 150-163
- Print publication:
- 30 April 1934
-
- Article
- Export citation
Torsion of beams whose cross-section is a regular polygon of n sides
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 139-149
- Print publication:
- 30 April 1934
-
- Article
- Export citation
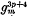 it is non-special and hence the redundancy of the base points is zero, therefore each of the double points of this system reduces the freedom by exactly three; and hence if we remove all the double points we get a system of curves of genus
it is non-special and hence the redundancy of the base points is zero, therefore each of the double points of this system reduces the freedom by exactly three; and hence if we remove all the double points we get a system of curves of genus