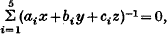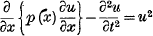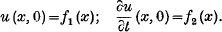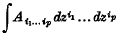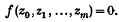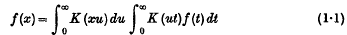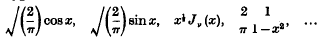Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
The Virial Theorem and the Theory of Strong Electrolytes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 2 / April 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 281-284
- Print publication:
- April 1935
-
- Article
- Export citation
The Number of Free Electrons in a Metal
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 2 / April 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 277-280
- Print publication:
- April 1935
-
- Article
- Export citation
A Statistical Derivation of Langmuir's Adsorption Isotherm
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 2 / April 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 260-264
- Print publication:
- April 1935
-
- Article
- Export citation
Geometrical Properties of Three Symmetric Matrices
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 2 / April 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 174-182
- Print publication:
- April 1935
-
- Article
- Export citation
The Mass of the Neutrino
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 2 / April 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 285-290
- Print publication:
- April 1935
-
- Article
- Export citation
The Electronic Structure of
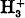
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 2 / April 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 244-259
- Print publication:
- April 1935
-
- Article
- Export citation
Limitations of Crystal Symmetry on Physical Phenomena with Particular Reference to Diamagnetic Magnetostriction
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 2 / April 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 265-270
- Print publication:
- April 1935
-
- Article
- Export citation
An Apparatus for Recording Average Amplitudes of Wireless Echoes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 2 / April 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 295-302
- Print publication:
- April 1935
-
- Article
- Export citation
The Effect of Non-Normality on the t Distribution
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 2 / April 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 223-231
- Print publication:
- April 1935
-
- Article
- Export citation
Note on the Equilibrium of Black-Body Radiation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 2 / April 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 242-243
- Print publication:
- April 1935
-
- Article
- Export citation
The Genus of a Developable Surface
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 2 / April 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 156-158
- Print publication:
- April 1935
-
- Article
- Export citation
A Note on the Hall and Magneto-Resistance Effects
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 2 / April 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 271-276
- Print publication:
- April 1935
-
- Article
- Export citation
PSP volume 31 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 2 / April 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- April 1935
-
- Article
- Export citation
Some Types of Irregular Surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 2 / April 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 159-173
- Print publication:
- April 1935
-
- Article
- Export citation
Cauchy's Problem in a Non-Linear Partial Differential Equation of Hyperbolic Type
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 2 / April 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 195-202
- Print publication:
- April 1935
-
- Article
- Export citation
Some Theorems on Abelian Integrals Associated with an Algebraic Variety
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 18-25
- Print publication:
- January 1935
-
- Article
- Export citation
Further Investigations of the Amplitude Variations of Downcoming Wireless Waves
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 125-144
- Print publication:
- January 1935
-
- Article
- Export citation
Note on a Paper of Bell and Wolfenden on Electrolytic Separation of Diplogen
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 116-118
- Print publication:
- January 1935
-
- Article
- Export citation
The Resultant of Two Fourier Kernels
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-6
- Print publication:
- January 1935
-
- Article
- Export citation
On the Resolution of Cremona Transformations and particularly those of Genus One in Space of Three Dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 31-47
- Print publication:
- January 1935
-
- Article
- Export citation