The protons emitted from boron, when it is bombarded by α-particles from radium C′ and polonium, have been examined. All have been ascribed to the disintegration of the B10 isotope following the capture of an α-particle. Four energy changes with values 3·1 m.v., 0·4 m.v., − 0·1 m.v., and − 1·0 m.v. are necessary to explain the range distribution observed. Experiments with α-particles from polonium also show that penetration through the top of the potential barrier stops at an energy of 3·6 m.v. and that below this there is a resonance level at about 2·9 m.v.

The flow due to a rotating disc. By W. G. Cochran.

In the footnote on p. 368 the third reference should be National Research Council, Bulletin No. 84, Hydrodynamics (1932), 280–2.

In recent years Cantor manifolds have assumed great importance in topology. This is due chiefly to the work of Urysohn and to the later work of Alexandroff. Urysohn, in the paper in which he introduced the theory of dimensions, showed that a 2-dimensional closed surface is a 2-dimensional Cantor manifold. Alexandroff has not only extended this result to n dimensions but has also established the existence on the cutting set Z of the surface F of generalized cycles homologous to zero on the various parts of F − Z. These results show that the deepest structural characteristics of the closed surface come to light when one dissects it.

In the first part of this paper I investigated the nature of the isolated singular points which can appear on an algebraic surface without affecting the conditions of adjunction and the arithmetic genus of the surface. It appeared that such points have neighbourhoods analysable into connected chains or trees of curves, each rational and of virtual grade − 2, and arranged either in a single chain (giving a binode, or a conic node if there is only one curve) or in three chains of, say, n, p, q curves respectively, one end curve of each chain meeting one which we may call the central curve of the tree. The values of n, p, q are not arbitrary, but satisfy either p = q = 1, or n ≤ 4, p = 2, q = 1; the unodes given by the former case we call U, those given by the latter case U, with a suffix indicating the reduction in class in each case. I pointed out the similarity between these results and Coxeter's enumeration of groups generated by reflexions, there being a one-one correspondence between these singularities and Coxeter's groups, with the restriction that the only groups with which we are concerned are those in which any two primes of symmetry are inclined at either π/2 or π/3. In fact, the curves which make up a complete neighbourhood correspond to the bounding primes of a fundamental region, two curves which do not meet corresponding to mutually perpendicular, primes, and two which do to primes inclined at π/3.

1. Die Fassung des lokalen Dimensionsbegriffes führt zu verschiedenen neuen, z. Teil schwierigen dimensionstheoretischen Strukturproblemen. In einer ganz natürlichen Weise ergeben sich dabei mehrere Gesichtspunkte je nach der Dimension des Raumes, in welchem die Gebilde eingebettet sind. Einer dieser Gesichtspunkte betrifft die n-dimens. Cantorschen Mannigfaltigkeiten (c.m.) in einem n-dimens. Raum; wir beginnen hier deren Untersuchung im einfachsten wesentlichen Fall—zweidimens. ebener Mannigfaltigkeiten. In dieser ersten Note werden wir beweisen, dass eine zweidimensionale c.m., welche von einer einzigen geschlossenen Kurve begrenzt wird, 1-dimensionale Mannigfaltigkeitsstellen dann und nur dann enthält, wenn die Begrenzungskurve keine einfache (Jordan-) Kurve ist. Damit wird eine Bedingung für das Auftreten 1-dimensionaler Mannigfaltigkeitsstellen gewonnen. Diese Stellen sind nämlich mit den nicht erreichbaren Randstellen des offenen Teiles der Mannigfaltigkeit identisch. Es ist bekannt, dass die hier behandelten speziellen c.m. noch schärfere Eigenschaften besitzen und deshalb sich mit viel schwächeren Begriffsbildungen erfassen lassen, nämlich unter dem Gesichtspunkt des Zusammenhangs im Kleinen. Demgegenüber sind die allgemeinen ebenen Mannigfaltigkeiten nicht erforscht und dort gelangt der lokale Dimensionsbegriff zu seiner Geltung. Die allgemeineren c.m. können ausserordentlich kompliziert sein, ja bereits im Falle, wo jeder Punkt der Mannigfaltigkeit ein 2-dimens. konzentrischer m.-Punkt ist. Die Gesichtspunkte, unter welchen sich solche c.m. behandeln lassen, sind vor allem der Zusammenhang einer ebenen c.m., die Anzahlihrer offenen Komponenten und insbesondere die Mehrfachheitihrer Punkte, je nach der (endl. oder unendlichen) Anzahl der nichtäquivalenten Folgen von c.m., welche einem 2-dimens.

A considerable amount of work has recently been done on the application of wave-mechanics to the theoretical study of chemical reactions. This has consisted chiefly in calculating activation energies and strengths of various bonds by consideration of electronic states in molecules. Some work has also been done on actual reaction mechanisms. It is evident from the latter that, owing to the large masses of the particles concerned, the quantum theory and the classical treatment will give different results only for reactions involving hydrogen or diplogen. Previous attempts to deal with such reactions have consisted simply of calculating the permeability G(W) of a barrier of height equal to the activation energy for protons of energy W. The reaction rate is then assumed to be given by

By an isolated singularity of an algebraic surface in [r] (i.e. space of r dimensions) I shall mean one which not merely is not upon any branch of a multiple curve of the surface, but has also the property that when the surface is projected into [3] from a general space [r − 4] the singular point remains in isolation, i.e. no branch of the double curve created by the projection will of necessity pass through it.

1·1. Let f (z) be an integral function of order ρ, and let

It is well known that, if ρ < 1,

This result was first conjectured by Littlewood, who proved it with cos 2πρ in place of cosπρ; it was afterwards proved independently by Wiman and Valiron about the same time. Many other authors have written on the subject, considering among other things the set of valves of r for which m (r) is comparatively large.

The problem of the enumeration of the different arrangements of n letters in an n × n Latin square, that is, in a square in which each letter appears once in every row and once in every column, was first discussed by Euler(1). A complete algebraic solution has been given by MacMahon(3) in two forms, both of which involve the action of differential operators on an expanded operand. If MacMahon's algebraic apparatus be actually put into operation, it will be found that different terms are written down, corresponding to all the different ways in which each row of the square could conceivably be filled up, that those arrangements which conflict with the conditions of the Latin square are ultimately obliterated, and those which conform to these conditions survive the final operation and each contribute unity to the result. The manipulation of the algebraic expressions, therefore, is considerably more laborious than the direct enumeration of the possible squares by a systematic and exhaustive series of trials. It is probably this circumstance which has introduced inaccuracies into the numbers of 5 × 5 and 6 × 6 Latin squares published in the literature.

An account is given of experiments to determine the polarisation of downcoming waves of long wavelength, using the method devised by Ratcliffe and White. The results show that on the whole the polarisation is left-handed, although there is a tendency for right-handed polarisation in the region of 1500 metres.

An apparatus for the production of beams of fast positive ions is described. Measurements of the cross-section for capture of an electron by a positive ion from a neutral gas atom are given on the case of He+ ions in helium and protons in helium and hydrogen. These are compared with the theory given by Massey and Smith, and as far as possible with previous experiments.

An improved circuit is described for a two thyratron counting unit such as is used in the “scale of two” thyratron counter. The advantages which result are that the minimum time of resolution is reduced and a source of occasional failure (“jamming”) of the counter is removed. Any type of impulse may be counted and, with selected thyratrons, impulses separated by only 0.00015 sec. may be reliably counted as separate. This makes possible a counting speed of 8000 random impulses per minute with a probable loss of only 2%.

The modification introduced into the circuit used in the original “scale of two” counter is that small condensers (0·0015 μF max) are cross connected between the grids and anodes of the pair of thyratrons, and the extinguishing condenser connected between the anodes is made small (0·02 μF max). The anode resistances are 10,000 ohms and grid leaks 100,000 ohms for the values of capacity mentioned. A valve amplifying stage is introduced, to pass the impulses from the modified circuit of the first pair to the second pair of thyratrons. For greater convenience the mechanical counting meter operated by the third pair is modified to count in multiples of eight so that no multiplication of its reading is necessary.

1. In a paper by Castelnuovo and Enriques the following fundamental theorem is proved:.

“An algebraic surface containing a linear system of curves of freedom r ≥ 0, genus π > 0, and grade n > 2π − 2 is necessarily scrollar.”

In the second part of this paper I pointed out how the presence of any singular point or points of the kind considered in the first part, on a rational surface, corresponds to a subgroup of the group of symmetry of the polytope which represents the properties of the system of base points in the plane representation of the surface. The subgroup is generated by reflexions, and may be the direct product of one or more factors (all the primes of symmetry in one factor being perpendicular to all those in any other factor). 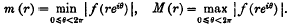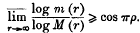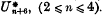Each factor corresponds to a singular point on the surface, namely (in Coxeter's notation), a factor [ ] to a conic node C2, a factor [3n] to a binode Bn+2 (n ≥ 1), a factor [3n,1,1] to a unode Un+5, (n ≥ 1), and finally a factor [3n,2,1] to a unode The possible subgroups in the finite groups that arise have been enumerated by Coxeter; and we shall find that every subgroup generated by reflexions in the group of symmetry of the polytope in ε dimensions which represents ε base points corresponds to a possible configuration of the base points, in which just those rational curves of grade − 2 are actual which correspond to primes of symmetry belonging to the subgroup; without exception, for ε ≤ 6; with one exception—the subgroup [ ]7—for ε = 7; and with three exceptions—the subgroups [ ]7, [ ]8, and [31,1,1 × [ ]4—for ε = 8. Since moreover the system |k| of cubics passing simply through all the base points is in all these cases an actually existing system, for which all the rational curves of grade − 2 are fundamental, its projective model (or in the case ε = 8, in which |k| is only a pencil, the projective model of the system |2k|) provides a rational surface on which all the sets of curves corresponding to the subgroups in question actually appear as singular points.

L. M. Milne-Thomson has recently described a method of solving linear finite difference equations by using processes some-what analogous to those employed by Heaviside.

The main object of this paper is to study the quadrics which have simultaneously certain poristic relations with a rational norm curve. We shall begin with a résumé of the work done in this direction in the ordinary space [3].

The most outstanding discrepancy between experiment and Dirac's theory of the electron is at present that shown by Dymond's experiments on the polarisation of beams of electrons by double scattering. It has been shown by Mott, using Dirac's relativistic wave equation, that one would expect a 15% asymmetry of beams of 140 k.v. electrons scattered twice at 90° by gold. The experiments of Dymond referred to above show that there cannot be more than 1% asymmetry. Several attempts have been made to explain this discrepancy, but without success. (For an account of these see Dymond's paper II.) One possibility which has not yet been investigated is that of exchange between the incident electron and the electrons of the struck atom. It is evident that only elastic exchange need be considered, since the probability of excitation of any form is known to be small. Only exchange with the K and L shells may be expected to give any appreciable effect.