Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
Thunderstorms and the penetrating radiation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 206-215
- Print publication:
- 30 April 1934
-
- Article
- Export citation
Experiments with a simple type of cloud chamber
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 201-205
- Print publication:
- 30 April 1934
-
- Article
- Export citation
The problem in statistics of testing several variances
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 164-169
- Print publication:
- 30 April 1934
-
- Article
- Export citation
The surfaces whose prime-sections contain a
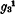
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 170-177
- Print publication:
- 30 April 1934
-
- Article
- Export citation
The gramophone horn
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 242-248
- Print publication:
- 30 April 1934
-
- Article
- Export citation
The heavy isotope of hydrogen. The Liversidge Lecture, 1934
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 225-241
- Print publication:
- 30 April 1934
-
- Article
- Export citation
Applications of lattice algebra
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 115-122
- Print publication:
- 30 April 1934
-
- Article
- Export citation
Note on the paper “On the combination of subalgebras*”
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, p. 200
- Print publication:
- 30 April 1934
-
- Article
- Export citation
The Petersen-Morley theorem, II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 197-199
- Print publication:
- 30 April 1934
-
- Article
- Export citation
The Petersen-Morley theorem, I
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 192-196
- Print publication:
- 30 April 1934
-
- Article
- Export citation
On smoothing and differentiation of tables
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 134-138
- Print publication:
- 30 April 1934
-
- Article
- Export citation
The optical properties of metals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 249-270
- Print publication:
- 30 April 1934
-
- Article
- Export citation
PSP volume 30 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- 30 April 1934
-
- Article
-
- You have access
- Export citation
PSP volume 30 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 2 / 30 April 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- 30 April 1934
-
- Article
-
- You have access
- Export citation
PSP volume 30 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 1 / January 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- January 1934
-
- Article
-
- You have access
- Export citation
An attempt to detect a neutral particle of small mass
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 1 / January 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 59-61
- Print publication:
- January 1934
-
- Article
- Export citation
The action of β and γ rays on rock salt crystals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 1 / January 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 62-69
- Print publication:
- January 1934
-
- Article
- Export citation
On points with arbitrarily assigned mutual distances
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 1 / January 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-3
- Print publication:
- January 1934
-
- Article
- Export citation
A figure in space of seven dimensions, and its sections
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 1 / January 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 19-26
- Print publication:
- January 1934
-
- Article
- Export citation
The theory of ionisation measurements in gases at high pressures
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 1 / January 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 80-101
- Print publication:
- January 1934
-
- Article
- Export citation
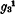
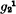 on the prime-sections. Thus, if we exclude ruled surfaces, they are rational surfaces. The supernormal surfaces are of order 4
on the prime-sections. Thus, if we exclude ruled surfaces, they are rational surfaces. The supernormal surfaces are of order 4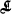 having the following properties:
having the following properties: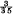 of the central fourth difference; or approximately by
of the central fourth difference; or approximately by 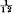 of the fourth difference. I have since found that the method had previously been suggested by Sir G. H. Darwin. It gives a great improvement in the steadiness of the differences and thereby makes interpolation much easier.
of the fourth difference. I have since found that the method had previously been suggested by Sir G. H. Darwin. It gives a great improvement in the steadiness of the differences and thereby makes interpolation much easier.

