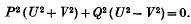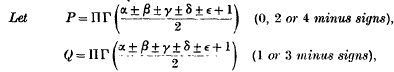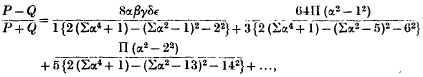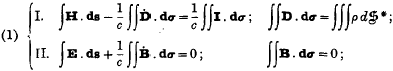Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
The Two-Dimensional Electrostatic Solutions of Born's new Field Equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 50-68
- Print publication:
- January 1935
-
- Article
- Export citation
Some Generalizations of Montel's Theorem
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 26-30
- Print publication:
- January 1935
-
- Article
- Export citation
An Attempt to Detect the Neutrino
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 99-107
- Print publication:
- January 1935
-
- Article
- Export citation
On a Class of Irregular Surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 48-49
- Print publication:
- January 1935
-
- Article
- Export citation
PSP volume 31 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- January 1935
-
- Article
-
- You have access
- Export citation
Ramanujan's Continued Fraction
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 7-17
- Print publication:
- January 1935
-
- Article
- Export citation
On Subdivisions of Complexes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 69-75
- Print publication:
- January 1935
-
- Article
- Export citation
On the Theory of Linear Integral Equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 76-84
- Print publication:
- January 1935
-
- Article
- Export citation
PSP volume 31 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- January 1935
-
- Article
-
- You have access
- Export citation
Ionization Power of a Neutrino with Magnetic Moment
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 108-115
- Print publication:
- January 1935
-
- Article
- Export citation
An Investigation of the Upper Limit of the Thorium C + C″ β-ray Spectrum by means of the Wilson Cloud Chamber
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 119-124
- Print publication:
- January 1935
-
- Article
- Export citation
Some Experiments on the Slowing Down of Neutrons by Collisions with Hydrogen Nuclei
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 145-152
- Print publication:
- January 1935
-
- Article
- Export citation
The Electric Moment of an Electron
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 94-98
- Print publication:
- January 1935
-
- Article
- Export citation
Phenomena Attending the Splashing of Water in an Electric Field
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 1 / January 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 85-93
- Print publication:
- January 1935
-
- Article
- Export citation
The fundamental equations of electromagnetism, independent of metrical geometry
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 4 / October 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 421-427
- Print publication:
- October 1934
-
- Article
- Export citation
The influence of screening on the creation and stopping of electrons
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 4 / October 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 524-539
- Print publication:
- October 1934
-
- Article
- Export citation
Finite groups generated by reflections, and their subgroups generated by reflections
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 4 / October 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 466-482
- Print publication:
- October 1934
-
- Article
- Export citation
PSP volume 30 issue 4 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 4 / October 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b10
- Print publication:
- October 1934
-
- Article
-
- You have access
- Export citation
On the regularity of surfaces, III
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 4 / October 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 404-408
- Print publication:
- October 1934
-
- Article
- Export citation
Torsion of beams of ⊥- and ∟- cross-sections
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 30 / Issue 4 / October 1934
- Published online by Cambridge University Press:
- 24 October 2008, pp. 392-403
- Print publication:
- October 1934
-
- Article
- Export citation