Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
Some Quartic Primals and Associated Cremona Transformations of Four-Dimensional Space
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 12-22
- Print publication:
- January 1936
-
- Article
- Export citation
The Relations between the Invariants of Two Surfaces in (1, n) Cyclic Correspondence
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 23-29
- Print publication:
- January 1936
-
- Article
- Export citation
Corrigendum
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, p. 183
- Print publication:
- January 1936
-
- Article
-
- You have access
- Export citation
On the Linearization of the Energy Density of the Electromagnetic Field
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 102-107
- Print publication:
- January 1936
-
- Article
- Export citation
On the Symmetries of the Solutions of a Certain Variational Problem
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 96-101
- Print publication:
- January 1936
-
- Article
- Export citation
On the Annihilation of Positrons
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 158-160
- Print publication:
- January 1936
-
- Article
- Export citation
The Gliding of a Plate on a Stream of Finite Depth. Part II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 67-85
- Print publication:
- January 1936
-
- Article
- Export citation
A Maximum-Minimum Method of Determining the Cardinal Points of a Lens System
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 138-143
- Print publication:
- January 1936
-
- Article
- Export citation
A Generalization of Picard's Method of Successive Approximation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 86-95
- Print publication:
- January 1936
-
- Article
- Export citation
On the Contacts of Circles
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-11
- Print publication:
- January 1936
-
- Article
- Export citation
PSP volume 32 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- January 1936
-
- Article
-
- You have access
- Export citation
Solution of a Moment Problem for Bounded Functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 30-39
- Print publication:
- January 1936
-
- Article
- Export citation
PSP volume 31 issue 4 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 4 / October 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- October 1935
-
- Article
-
- You have access
- Export citation
A Connection between Correlation and Contingency
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 4 / October 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 520-524
- Print publication:
- October 1935
-
- Article
- Export citation
On the Structure of Abstract Algebras
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 4 / October 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 433-454
- Print publication:
- October 1935
-
- Article
- Export citation
Some Experiments with Neutrons slowed down at different Temperatures
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 4 / October 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 617-624
- Print publication:
- October 1935
-
- Article
- Export citation
Discussion of Probability Relations between Separated Systems
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 4 / October 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 555-563
- Print publication:
- October 1935
-
- Article
- Export citation
On a Uniqueness Theorem
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 4 / October 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 625-628
- Print publication:
- October 1935
-
- Article
- Export citation
On the Virtual Grade of Curves on an Algebraic Surface
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 4 / October 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 536-542
- Print publication:
- October 1935
-
- Article
- Export citation
Note on the development of the Circulation around a thin Elliptic Cylinder
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 31 / Issue 4 / October 1935
- Published online by Cambridge University Press:
- 24 October 2008, pp. 582-584
- Print publication:
- October 1935
-
- Article
- Export citation
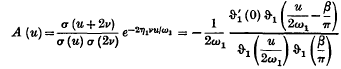
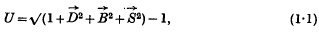
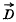 is the electric displacement,
is the electric displacement, 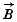 the magnetic induction,
the magnetic induction, 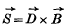 the Poynting vector) with the help of the commutation laws for these vectors.
the Poynting vector) with the help of the commutation laws for these vectors.
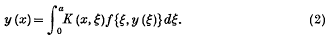

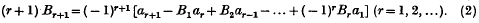
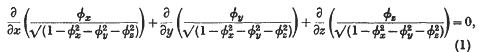
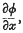 etc.
etc.