Let a1, a2, … be a sequence of variables. Write

We use the notation Bn = Bn (a1, …, an) to indicate the variables on which Bn depends.

The dissociation of hydrogen by a hot tungsten filament has been studied under conditions such that all the atomic hydrogen produced is effectively removed by reaction with molybdenum or tungsten oxide. The rate of production of atomic hydrogen is many times greater than was inferred from earlier work. With the tungsten at constant temperature the rate of dissociation is proportional to the square root of the pressure. A formula is given for the rate of production of hydrogen atoms per sq. cm. of the tungsten per second.

When a probability distribution is specified by more than one parameter, the statistical information in a sample on an unknown α will usually depend on the values of the other unknowns. For large samples where the joint distribution of the estimates tends to normality, and the efficiency of the estimation to a maximum, little theoretical difficulty exists. In a discussion(1) of the more general theory of small samples, I have stressed the importance of properties of sufficiency.

The results of experiments on the diffusion of hydrogen through metals from a pressure p on one side to a vacuum on the other show that at high pressures the amount diffusing varies linearly with p½ but that at low pressures it varies more rapidly. The difficulty usually encountered when diffusion from an adsorbed layer into the solid is considered theoretically is that the theory indicates that saturation should be reached. In this paper it is shown that this difficulty is due to the omission of an important process at the surface and that by including this process the experimental results can be explained.

In this paper we consider the slow two-dimensional motion of viscous liquid past a sharp edge projecting into and normal to the undisturbed direction of the stream. The liquid is supposed bounded by rigid planes represented by ABCDE in Fig. 1, and, apart from the disturbance caused by the projection, is assumed to be in uniform shearing motion. The stream function is then a bi-harmonic function that must vanish together with its normal derivative at all points of the boundary, and must be proportional to y2 at a great distance from the projection.

The Abel sum of the series can be written in the form

where

This suggests that we should define the “Abel limit”, as u → ∞, of any function A(u) as being given by the expression (1) whenever this exists. We shall, however, in this paper, restrict ourselves to functions A(u) which are bounded in any finite interval. Since we are concerned only with the behaviour of A(u) as u → ∞, this does not involve any serious loss of generality, while we avoid difficulties arising from the divergence of integrals at finite points. 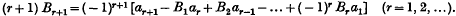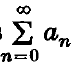We note that the expression (1) can be written in the form

where

A1(u) may conveniently be described as the “Abel transform” of A(u).

When an electron makes a transition from a continuous state to a bound state, for example in the case of neutralization of a positive ion or formation of a negative ion, its excess energy must be disposed of in some way. It is usually given off as radiation. In the case of neutralization of positive ions the radiation forms the well-known continuous spectrum. No such spectrum due to the direct formation of negative ions has, however, been observed. This process has been fully discussed in a recent paper by Massey and Smith. It is shown that in this case the spectrum would be difficult to observe.

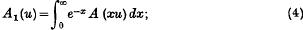
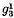1. In 1891, Castelnuovo suggested that there may exist canonical surfaces which consist of three sheets covering the same surface. In particular, he remarked that, if the canonical curves of a surface contain a then the canonical model of the surface is certainly a three-sheeted surface. An example is the quintic surface with a tacnode, in space of three dimensions; its canonical model is a triple plane, branching along a curve of order 12 with twenty-four cusps which lie on a quartic.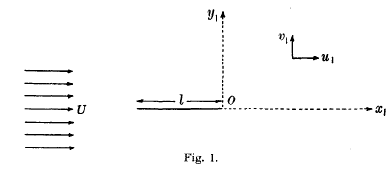

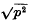1. The velocity distribution in fluid of small viscosity, or at large Reynolds number, in the laminar boundary layer associated with a thin flat plate along the main direction of flow, has been worked out by Blasius on the basis of the Prandtl theory. These original investigations covered the region from the forward edge of the plate to the downstream edge. In a recent paper Goldstein investigated the velocity distribution in the wake immediately behind the downstream edge over a region within about 0·5l from it, l being the length of the plate. Later

Tollmien obtained a first approximation to the flow at a great distance down-stream. Goldstein § extended Tollmien's solution by finding a second approximation and by joining it up with his previous work on the flow very near the plate.

Experiments are described in which observations were made of the motion of electrically charged cloud particles past a sphere. The cloud particles were moving vertically up in an air stream, and there was a vertical electric field. This gave conditions similar to those surrounding a falling rain drop in a thundercloud, and the observations are in accordance with the theory proposed by Wilson to account for the mechanism of thunderclouds.

As particular cases of the general problem of finding the most general limiting tangential form of a degenerate manifold, we discuss here the degeneration of a curve on a surface into one or more multiple components, and the degeneration of a surface on a threefold into a single surface counting multiply, the method used consisting essentially in finding the approximate form of the curve or surface as the limit is approached. The approach system is supposed in all cases to be contained in a linear system of curves or surfaces, on the surface or threefold considered.

J. A. Todd has enunciated the following theorem:

“If the canonical adjoints ∑ of an irreducible curve Γ contain fixed parts, then, if Γ is not elliptic, all the fixed curves are simple, rational, determined uniquely by the base points, which present independent conditions for them, and have no free intersections with each other or with the variable part of the system ∑.”

In a previous paper (2) by one of the authors some types of periodic potential functions were obtained and were applied to problems in which the boundaries were cylinders or spheres arranged at regular intervals in a row or ring. It is now our object to extend the methods of that paper to a number of other cases.

Ising discussed the following model of a ferromagnetic body: Assume N elementary magnets of moment μ to be arranged in a regular lattice; each of them is supposed to have only two possible orientations, which we call positive and negative. Assume further that there is an interaction energy U for each pair of neighbouring magnets of opposite direction. Further, there is an external magnetic field of magnitude H such as to produce an additional energy of − μH (+ μH) for each magnet with positive (negative) direction.

In the general systems of vortices represented by (1) the mean variation in pressure is

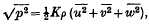
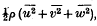where K is a number which varies between 1 and √2. When the vortices are confined to cubical partitions, the case most nearly analogous to that of free turbulence, K = 1·06, so that the conjecture which I made some years ago, that would be equal to is probably nearly correct.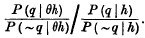

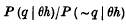
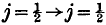In a previous paper (afterwards referred to as Paper I) tests have been given for the significance of some quantities found statistically. The results are given in the form P(q | θh)/P (˜ q|θh); here h denotes the previous knowledge and θ the experimental evidence used, while q is the hypothesis that all the variations outstanding can be attributed to accidental error or random variation, and ˜q the hypothesis that at least part of them is systematic. It has been supposed in the analysis that q and ˜q are equally probable on the information h; but if they are not, the only alteration is that the ratios evaluated now represent

If successive batches of relevant information are available the total effect on the probability of q can therefore be got by multiplying the values of

given by the investigations separately. In each case the assumption that q has prior probability ½ is really a practical working rule rather than a statement of fact.

The intensities of X-ray spectral lines resulting from transitions between the K, L and M shells have been calculated using screened relativistic wave functions. The relativistic modifications are shown to decrease the Lβ3β4 doublet ratio but do not alter the Kα1α2 and Kβ1β3 ratios, in agreement with experiment. The calculated intensities of the forbidden lines arising from quadrupole transitions are in good agreement with experiment. Lines due to transitions arising from the magnetic dipole moment of the electron are found to be very weak, but the LI → K transition might just be observable for heavy elements.