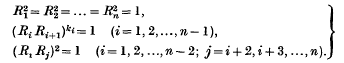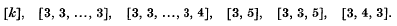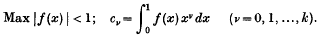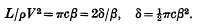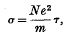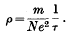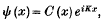Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
On surfaces of sectional genus six
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 3 / October 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 355-365
- Print publication:
- October 1936
-
- Article
- Export citation
Statistical theory of adsorption with interaction between the adsorbed atoms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 3 / October 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 471-476
- Print publication:
- October 1936
-
- Article
- Export citation
Probability relations between separated systems
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 3 / October 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 446-452
- Print publication:
- October 1936
-
- Article
- Export citation
Note on hyperelliptic surfaces and certain kummer surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 3 / October 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 342-354
- Print publication:
- October 1936
-
- Article
- Export citation
Second-order focusing for the mass spectrograph
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 3 / October 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 453-460
- Print publication:
- October 1936
-
- Article
- Export citation
Note on optical methods of measuring the size of small water drops
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 3 / October 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 493-498
- Print publication:
- October 1936
-
- Article
- Export citation
The magnetic properties of antimony
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 3 / October 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 499-502
- Print publication:
- October 1936
-
- Article
- Export citation
Boundary layer growth
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 3 / October 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 392-401
- Print publication:
- October 1936
-
- Article
- Export citation
An attempt to produce artificial radioactivity by an electron beam, with some notes on the behaviour of newly made Geiger-Muller counters
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 3 / October 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 503-505
- Print publication:
- October 1936
-
- Article
- Export citation
A theorem on algebraic correspondences
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 3 / October 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 337-341
- Print publication:
- October 1936
-
- Article
- Export citation
PSP volume 32 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- May 1936
-
- Article
-
- You have access
- Export citation
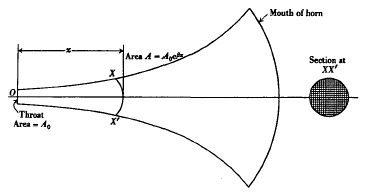
Transient Oscillations in a Loud-Speaker Horn
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 265-275
- Print publication:
- May 1936
-
- Article
- Export citation
Abstract Definitions for the Symmetry Groups of the Regular Polytopes, in Terms of Two Generators. Part I: The Complete Groups
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 194-200
- Print publication:
- May 1936
-
- Article
- Export citation
On the Proof of a Lemma Enunciated by Severi
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 253-259
- Print publication:
- May 1936
-
- Article
- Export citation
On the Fourier Constants of a Bounded Function
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 201-211
- Print publication:
- May 1936
-
- Article
- Export citation
On the Geometrical Genus of Certain Surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 185-193
- Print publication:
- May 1936
-
- Article
- Export citation
Note on the Gliding of a Plate on the Surface of a Stream
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 248-252
- Print publication:
- May 1936
-
- Article
- Export citation
The Electrical Resistance of Dilute Solid Solutions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 281-290
- Print publication:
- May 1936
-
- Article
- Export citation
Determination of the Energy Distribution of Recoil Atoms During β Decay and the Existence of the Neutrino
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 301-303
- Print publication:
- May 1936
-
- Article
- Export citation
Elementary Theory of the Critical Field of a Dielectric
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 276-280
- Print publication:
- May 1936
-
- Article
- Export citation