Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
Selection Rules in Nuclear Radiation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 291-300
- Print publication:
- May 1936
-
- Article
- Export citation
On the Decomposition of an Infinitesimal Group
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 229-237
- Print publication:
- May 1936
-
- Article
- Export citation
PSP volume 32 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- May 1936
-
- Article
-
- You have access
- Export citation
The Response of a Non-Linear Electric Circuit to an Impulse
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 304-320
- Print publication:
- May 1936
-
- Article
- Export citation
On the Extension of the Pflastersatz
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 238-247
- Print publication:
- May 1936
-
- Article
- Export citation
A Remark on Fourier Transforms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 321-327
- Print publication:
- May 1936
-
- Article
- Export citation
The Intensity of the γ-Rays emitted by the Active Deposit of Thorium
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 328-335
- Print publication:
- May 1936
-
- Article
- Export citation
On Order in Time
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 216-228
- Print publication:
- May 1936
-
- Article
- Export citation
The Polarizability of Molecular Hydrogen H2
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 260-264
- Print publication:
- May 1936
-
- Article
- Export citation
The Meromorphisms of an Elliptic Function-Field
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 2 / May 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 212-215
- Print publication:
- May 1936
-
- Article
- Export citation
The Stability of Viscous Fluid Flow under Pressure between Parallel Planes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 40-54
- Print publication:
- January 1936
-
- Article
- Export citation
PSP volume 32 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- January 1936
-
- Article
-
- You have access
- Export citation
Thermal Properties of an Incompletely Degenerate Fermi Gas
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 108-111
- Print publication:
- January 1936
-
- Article
- Export citation
On the Stability Problem in Hydrodynamics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 55-66
- Print publication:
- January 1936
-
- Article
- Export citation
On the Radiation Emitted by a Multipole and its Angular Momentum
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 112-126
- Print publication:
- January 1936
-
- Article
- Export citation
The Errors of Approximation in Jeffreys's Phases
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 161-178
- Print publication:
- January 1936
-
- Article
- Export citation
Adsorption Isotherms. Critical Conditions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 144-151
- Print publication:
- January 1936
-
- Article
- Export citation
Experiments on the Efficiencies of Production and the Half-Lives of Radio-Carbon and Radio-Nitrogen
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 179-182
- Print publication:
- January 1936
-
- Article
- Export citation
The New Action Function and the Unitary Field Theory
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 127-137
- Print publication:
- January 1936
-
- Article
- Export citation
The Dissociation Equilibrium of Hydrogen and its Adsorption on Tungsten
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 32 / Issue 1 / January 1936
- Published online by Cambridge University Press:
- 24 October 2008, pp. 152-157
- Print publication:
- January 1936
-
- Article
- Export citation
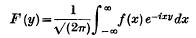
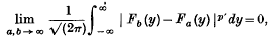
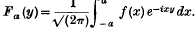
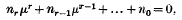
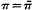 (which is equivalent to |
(which is equivalent to |

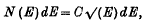
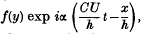 , it is found that, for small Reynolds numbers
, it is found that, for small Reynolds numbers 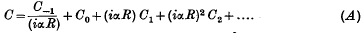
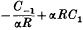 in this approximation, is found to be positive. When α is of the order of unity, the value of
in this approximation, is found to be positive. When α is of the order of unity, the value of 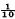 of the first is about 50 for the symmetrical disturbance and 100 for the antisymmetrical disturbance.
of the first is about 50 for the symmetrical disturbance and 100 for the antisymmetrical disturbance. 
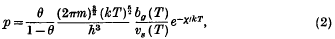
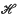 as an action function. This new form of the variational principle enables us to find a new special action function, which conserves the chief features of Born's theory while changing some of its former results. To a given charge correspond two static solutions with central symmetry, one giving a finite, the other an infinite energy. The potential of the one (light) particle is analogous to that in Born's theory while the potential of the other resembles a potential barrier. Also, by using the new action function, the symmetry between electric and magnetic fields ceases to exist.
as an action function. This new form of the variational principle enables us to find a new special action function, which conserves the chief features of Born's theory while changing some of its former results. To a given charge correspond two static solutions with central symmetry, one giving a finite, the other an infinite energy. The potential of the one (light) particle is analogous to that in Born's theory while the potential of the other resembles a potential barrier. Also, by using the new action function, the symmetry between electric and magnetic fields ceases to exist.