Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
The second order electrical effects in metals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 371-379
- Print publication:
- July 1937
-
- Article
- Export citation
The effect of temperature on the reflexion of X-rays
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 380-384
- Print publication:
- July 1937
-
- Article
- Export citation
A critical examination of Benedicks' homogeneous electro-thermal effect
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 385-389
- Print publication:
- July 1937
-
- Article
- Export citation
On temperature in relation to quantal phenomena
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 340-343
- Print publication:
- July 1937
-
- Article
- Export citation
PSP volume 33 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- July 1937
-
- Article
-
- You have access
- Export citation
On an inequality in the elementary theory of numbers
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 2 / April 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 207-209
- Print publication:
- April 1937
-
- Article
- Export citation
A comparison of wave functions for the normal helium atom
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 2 / April 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 253-259
- Print publication:
- April 1937
-
- Article
- Export citation
PSP volume 33 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 2 / April 1937
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- April 1937
-
- Article
-
- You have access
- Export citation
A note on molecular orbitals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 2 / April 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 250-252
- Print publication:
- April 1937
-
- Article
- Export citation
The effect of configuration interaction on the low terms of the spectra of oxygen
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 2 / April 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 240-249
- Print publication:
- April 1937
-
- Article
- Export citation
An infinite integral involving Bessel functions and parabolic cylinder functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 2 / April 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 210-211
- Print publication:
- April 1937
-
- Article
- Export citation
PSP volume 33 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 2 / April 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- April 1937
-
- Article
-
- You have access
- Export citation
The “closest” estimates of statistical parameters
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 2 / April 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 212-222
- Print publication:
- April 1937
-
- Article
- Export citation
On an equation occurring in Falkner and Skan's approximate treatment of the equations of the boundary layer
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 2 / April 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 223-239
- Print publication:
- April 1937
-
- Article
- Export citation
Superconducting cylinders
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 2 / April 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 260-276
- Print publication:
- April 1937
-
- Article
- Export citation
The generalized Fermi interaction
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 2 / April 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 277-292
- Print publication:
- April 1937
-
- Article
- Export citation
The envelope of the subspaces of the polyhedra of an involution on a rational curve
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 2 / April 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 183-187
- Print publication:
- April 1937
-
- Article
- Export citation
On certain surfaces which have unpostulated singularities
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 2 / April 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 199-206
- Print publication:
- April 1937
-
- Article
- Export citation
Projective characters and invariants of algebraic varieties
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 2 / April 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 188-198
- Print publication:
- April 1937
-
- Article
- Export citation
The β- and γ-radiation of RaC″
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 1 / March 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 154-163
- Print publication:
- March 1937
-
- Article
- Export citation


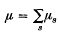 and μ
and μ