Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
Note on an identity connected with diophantine approximation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, p. 27
- Print publication:
- January 1938
-
- Article
- Export citation
Lattice changes associated with the formation of superlattices in alloys
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 81-88
- Print publication:
- January 1938
-
- Article
- Export citation
On the velocity and temperature distributions in the turbulent wake behind a heated body of revolution
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 48-67
- Print publication:
- January 1938
-
- Article
- Export citation
PSP volume 34 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- January 1938
-
- Article
-
- You have access
- Export citation
The Hankel transform of Whittaker's function Wk, m(z)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 28-29
- Print publication:
- January 1938
-
- Article
- Export citation
A “Scale-of-two” High-Speed Counter Using Hard Vacuum Triodes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 549-558
- Print publication:
- October 1937
-
- Article
- Export citation
Superconductors in Alternating Magnetic Fields
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 559-576
- Print publication:
- October 1937
-
- Article
- Export citation
Two-Dimensional Potential Problems
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 474-484
- Print publication:
- October 1937
-
- Article
- Export citation
An A.C. Method of Measuring Resistance
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 577-582
- Print publication:
- October 1937
-
- Article
- Export citation
Specific Heats of Solids due to Molecular Rotations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 524-533
- Print publication:
- October 1937
-
- Article
- Export citation
The Dependence on Composition of the Critical Ordering Temperature in Alloys
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 502-517
- Print publication:
- October 1937
-
- Article
- Export citation
Statement of Accounts of the Cambridge Philosophical Society, from January 1, 1936, to December 31, 1936
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 595-596
- Print publication:
- October 1937
-
- Article
- Export citation
The Elastic Stability of a Corrugated Plate Under a Shearing Force
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 459-473
- Print publication:
- October 1937
-
- Article
- Export citation
On the Smoothing of Observed Data
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 444-450
- Print publication:
- October 1937
-
- Article
- Export citation
Note on the Invariants of the Canonical System of an Algebraic Variety
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 438-443
- Print publication:
- October 1937
-
- Article
- Export citation
PSP volume 33 issue 4 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f8
- Print publication:
- October 1937
-
- Article
-
- You have access
- Export citation
The Radioactivity Produced by the Bombardment of Lithium with Deuterons
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 534-539
- Print publication:
- October 1937
-
- Article
- Export citation
The Spectrum of the Normal Frequencies of a Polar Linear Lattice
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 485-501
- Print publication:
- October 1937
-
- Article
- Export citation
The Application of the Electron Lens to Cloud Chamber Photography
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 540-548
- Print publication:
- October 1937
-
- Article
- Export citation
Proceedings at the Meetings Held During the Session 1936–1937 Annual General Meeting
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 586-591
- Print publication:
- October 1937
-
- Article
- Export citation
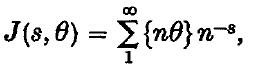
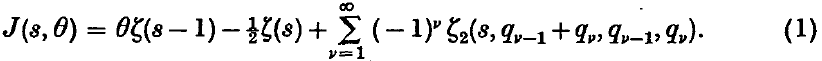
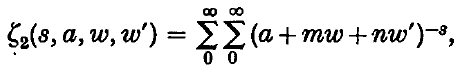
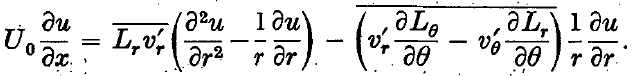
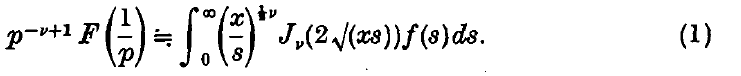
 sec. for a sphere of about 1 cm. diameter.
sec. for a sphere of about 1 cm. diameter. by protons, resulting in the emission of three α-particles, Dee and Gilbert* found that the observed distributions of ranges and angles of these particles could be explained by assuming that one α-particle is first ejected, leaving a short-lived, excited
by protons, resulting in the emission of three α-particles, Dee and Gilbert* found that the observed distributions of ranges and angles of these particles could be explained by assuming that one α-particle is first ejected, leaving a short-lived, excited  nucleus which then decomposes into two more α-particles. The half-life of this excited beryllium nucleus was estimated to be about 10
nucleus which then decomposes into two more α-particles. The half-life of this excited beryllium nucleus was estimated to be about 10