Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
Concerning secondary flow in straight pipes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 335-344
- Print publication:
- July 1938
-
- Article
- Export citation
Note on the velocity and temperature distributions behind a heated body of revolution
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 351-353
- Print publication:
- July 1938
-
- Article
- Export citation
Velocity and temperature distributions in the turbulent wake behind a heated body of revolution
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 345-350
- Print publication:
- July 1938
-
- Article
- Export citation
An extension of a theorem of Kulakoff
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 316-320
- Print publication:
- July 1938
-
- Article
- Export citation
Variation of ionization with range of α-particles, protons, deuterons and 3H particles
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 450-458
- Print publication:
- July 1938
-
- Article
- Export citation
Absorption and coincidence experiments on the radiations from the radioactive sodium, Na24
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 442-449
- Print publication:
- July 1938
-
- Article
- Export citation
The disintegration of boron by slow neutrons
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 290-295
- Print publication:
- April 1938
-
- Article
- Export citation
A discussion of the thermal expansion and conductivity in liquid helium II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 253-261
- Print publication:
- April 1938
-
- Article
- Export citation
Superlattice formation of the type AB in alloys with applications to the theory of adsorption
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 224-237
- Print publication:
- April 1938
-
- Article
- Export citation
Birational transformations possessing fundamental curves
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 144-155
- Print publication:
- April 1938
-
- Article
- Export citation
The use of minimum χ2 as an approximation to the method of maximum likelihood
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 156-157
- Print publication:
- April 1938
-
- Article
- Export citation
The internal conversion electrons of actinon
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 282-289
- Print publication:
- April 1938
-
- Article
- Export citation
PSP volume 34 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- April 1938
-
- Article
-
- You have access
- Export citation
The surface tension of liquid helium
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 299-300
- Print publication:
- April 1938
-
- Article
- Export citation
Further experiments on the slow neutrons transmitted by cadmium: influence of the temperature of the slowing down medium
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 272-281
- Print publication:
- April 1938
-
- Article
- Export citation
Über die monotone Konvergenz der Cesàro-Mittel bei Fourier- und Potenzreihen
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 134-143
- Print publication:
- April 1938
-
- Article
- Export citation
The velocity of sound in liquid nitrogen
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 296-298
- Print publication:
- April 1938
-
- Article
- Export citation
Self-consistent field for molecular hydrogen
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 204-212
- Print publication:
- April 1938
-
- Article
- Export citation
Concerning the velocity and temperature distributions in plane and axially symmetrical jets
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 185-203
- Print publication:
- April 1938
-
- Article
- Export citation
Statistical theory of adsorption with long-range interaction
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 238-252
- Print publication:
- April 1938
-
- Article
- Export citation
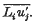 It is shown that a secondary motion arises if the mixture length is not constant on the curves along which | grad
It is shown that a secondary motion arises if the mixture length is not constant on the curves along which | grad 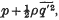 where
where 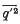 is the mean value of the square of the velocity fluctuation and
is the mean value of the square of the velocity fluctuation and 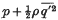 across the channel from the central plane to each wall. Qualitative arguments such as are used to explain the existence of a secondary flow for laminar motion in a curved pipe are applied here to show that a secondary flow is to be expected near the short sides in the turbulent flow through a straight rectangular pipe of large length/breadth ratio.
across the channel from the central plane to each wall. Qualitative arguments such as are used to explain the existence of a secondary flow for laminar motion in a curved pipe are applied here to show that a secondary flow is to be expected near the short sides in the turbulent flow through a straight rectangular pipe of large length/breadth ratio.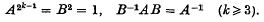
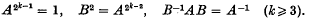
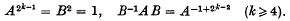
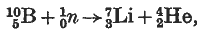

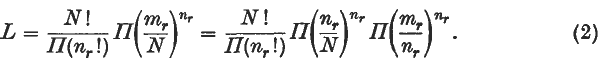

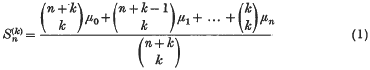
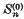 die
die 