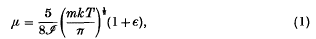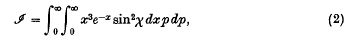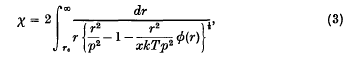Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
The Shot Effect for Showers
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 451-458
- Print publication:
- October 1937
-
- Article
- Export citation
Intersections of Loci on an Algebraic V4
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 425-437
- Print publication:
- October 1937
-
- Article
- Export citation
Quelques Remarques à Propos D'Une Note De G. H. Hardy: The Resultant of two Fourier Kernels (1)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 413-418
- Print publication:
- October 1937
-
- Article
- Export citation
Note on a Theorem of Myrberg
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 419-424
- Print publication:
- October 1937
-
- Article
- Export citation
Hopkins prize, Award, 1930–1933
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 592-594
- Print publication:
- October 1937
-
- Article
- Export citation
The “Overshoot Phenomenon” in Superconductivity
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 583-585
- Print publication:
- October 1937
-
- Article
- Export citation
The Statistics of the Hydrogen-Palladium System
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 4 / October 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 518-523
- Print publication:
- October 1937
-
- Article
- Export citation
The numerical calculation of

-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 359-362
- Print publication:
- July 1937
-
- Article
- Export citation
On the canonical systems of certain algebraic surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 311-314
- Print publication:
- July 1937
-
- Article
- Export citation
The effect of two isolated forces on the elastic stability of a flat rectangular plate
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 325-339
- Print publication:
- July 1937
-
- Article
- Export citation
The theory of the single-pass cross-flow heat interchanger
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 403-411
- Print publication:
- July 1937
-
- Article
- Export citation
Note on the derivation of fluctuation formulae for statistical assemblies
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 390-393
- Print publication:
- July 1937
-
- Article
- Export citation
A symmetrical configuration of n + 1 rational normal curves in [2n]
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 293-300
- Print publication:
- July 1937
-
- Article
- Export citation
Regular canonical surfaces of genus three and four
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 306-310
- Print publication:
- July 1937
-
- Article
- Export citation
The theory of the shot effect. II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 344-358
- Print publication:
- July 1937
-
- Article
- Export citation
Abstract definitions for the symmetry groups of the regular polytopes, in terms of two generators. Part II: the rotation groups
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 315-324
- Print publication:
- July 1937
-
- Article
- Export citation
The determination of intermolecular forces in gases from their viscosity
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 363-370
- Print publication:
- July 1937
-
- Article
- Export citation
A study of the properties of hydrogen films on tungsten by the method of contact potentials
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 394-402
- Print publication:
- July 1937
-
- Article
- Export citation
PSP volume 33 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- July 1937
-
- Article
-
- You have access
- Export citation
The postulation of a multiple surface
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 33 / Issue 3 / July 1937
- Published online by Cambridge University Press:
- 24 October 2008, pp. 301-305
- Print publication:
- July 1937
-
- Article
- Export citation


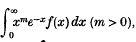 is of frequent occurrence in problems in the kinetic theory of gases and in particular is required in the paper which follows, in calculating viscosity. The result is an extension of one given by Berger, and the analysis follows closely the discussion of Gauss's formula for approximate quadrature in Whittaker and Robinson,
is of frequent occurrence in problems in the kinetic theory of gases and in particular is required in the paper which follows, in calculating viscosity. The result is an extension of one given by Berger, and the analysis follows closely the discussion of Gauss's formula for approximate quadrature in Whittaker and Robinson, 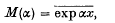

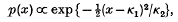

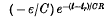 to the anode potential of the valve whose anode to earth capacity is
to the anode potential of the valve whose anode to earth capacity is