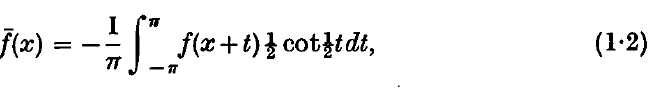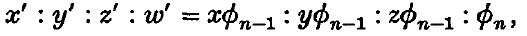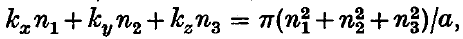Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
The evaporation of concentrated films of sodium
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 262-271
- Print publication:
- April 1938
-
- Article
- Export citation
The moment of the fluid forces acting on a plate which is gliding on the surface of a stream
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 167-184
- Print publication:
- April 1938
-
- Article
- Export citation
The shot effect with space charge
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 158-166
- Print publication:
- April 1938
-
- Article
- Export citation
The diffraction of light by supersonic waves in solids
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 213-223
- Print publication:
- April 1938
-
- Article
- Export citation
Proof of a theorem of Paley
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 125-133
- Print publication:
- April 1938
-
- Article
- Export citation
PSP volume 34 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- April 1938
-
- Article
-
- You have access
- Export citation
Thermal equilibrium at temperatures below 1° absolute
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 2 / April 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 301-307
- Print publication:
- April 1938
-
- Article
- Export citation
A search for ionization of hydrogen by diffusion through palladium
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 120-123
- Print publication:
- January 1938
-
- Article
- Export citation
The resolution of monoidal Cremona transformations of three-dimensional space
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 22-26
- Print publication:
- January 1938
-
- Article
- Export citation
Soft X-ray bands from dilute alloys
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 109-114
- Print publication:
- January 1938
-
- Article
- Export citation
Fiducial distribution of several parameters with application to a normal system
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 41-47
- Print publication:
- January 1938
-
- Article
- Export citation
PSP volume 34 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- January 1938
-
- Article
-
- You have access
- Export citation
The conductivity of thin metallic films according to the electron theory of metals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 100-108
- Print publication:
- January 1938
-
- Article
- Export citation
The critical ordering temperature in alloys. II. The existence of a two-phase region
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 68-80
- Print publication:
- January 1938
-
- Article
- Export citation
The expansion of an arbitrary function in a series of conal or toroidal functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 30-32
- Print publication:
- January 1938
-
- Article
- Export citation
Further aspects of the theory of multiple regression
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 33-40
- Print publication:
- January 1938
-
- Article
- Export citation
Determinantal representations of x4+y4+z4
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 6-21
- Print publication:
- January 1938
-
- Article
- Export citation
Electronic energy bands in metallic copper and silver
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 89-99
- Print publication:
- January 1938
-
- Article
- Export citation
The fixed part of the canonical system on an algebraic surface
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-5
- Print publication:
- January 1938
-
- Article
- Export citation
Note on the absorption limits for the primary β-particles of mesothorium 2 and uranium X2
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 1 / January 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 115-119
- Print publication:
- January 1938
-
- Article
- Export citation
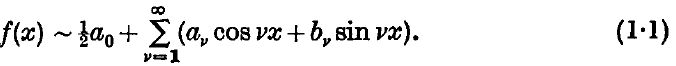
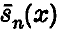 and
and 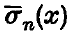 we denote the partial sums and the first arithmetic means of the series
we denote the partial sums and the first arithmetic means of the series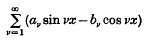
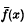 we mean the function conjugate to
we mean the function conjugate to