Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
Note on the production of positron-electron pairs during the passage of β-particles through matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 435-441
- Print publication:
- July 1938
-
- Article
- Export citation
The effect of departures from ideal conditions other than non-normality on the t and z tests of significance
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 321-328
- Print publication:
- July 1938
-
- Article
- Export citation
The binding energies of the hydrogen isotopes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 365-374
- Print publication:
- July 1938
-
- Article
- Export citation
Note on fluctuations and the shot effect
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 329-334
- Print publication:
- July 1938
-
- Article
- Export citation
PSP volume 34 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- July 1938
-
- Article
-
- You have access
- Export citation
A modernized version of Gibbs' use of the grand canonical ensemble
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 382-391
- Print publication:
- July 1938
-
- Article
- Export citation
Anomalous scattering of α-particles and long-range nuclear forces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 498-501
- Print publication:
- July 1938
-
- Article
- Export citation
A note on the melting-point of paraffins and fatty acids
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 459-464
- Print publication:
- July 1938
-
- Article
- Export citation
On the energies associated with the two-centre problem: I. General features of the energy surface
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 375-381
- Print publication:
- July 1938
-
- Article
- Export citation
The thermal conductivity of metals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 474-497
- Print publication:
- July 1938
-
- Article
- Export citation
Contributions to the statistical theory of adsorption: I. The elementary theory of adsorption in a first and second layer
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 392-398
- Print publication:
- July 1938
-
- Article
- Export citation
The “overshoot phenomenon” in superconductivity
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 465-469
- Print publication:
- July 1938
-
- Article
- Export citation
PSP volume 34 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- July 1938
-
- Article
-
- You have access
- Export citation
The kinetics of adsorption with long-range interaction between adsorbed particles
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 412-423
- Print publication:
- July 1938
-
- Article
- Export citation
A further note on Ramanujan's arithmetical function τ(n)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 309-315
- Print publication:
- July 1938
-
- Article
- Export citation
An apparatus for recording the strength of wireless signals from a Morse sender
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 470-473
- Print publication:
- July 1938
-
- Article
- Export citation
A note on an assumption in the theory of cooperative phenomena
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 424-428
- Print publication:
- July 1938
-
- Article
- Export citation
The charge-dependence of nuclear forces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 354-364
- Print publication:
- July 1938
-
- Article
- Export citation
Corrigendum
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, p. 502
- Print publication:
- July 1938
-
- Article
-
- You have access
- Export citation
Some properties of mobile and immobile adsorbed films
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 34 / Issue 3 / July 1938
- Published online by Cambridge University Press:
- 24 October 2008, pp. 399-411
- Print publication:
- July 1938
-
- Article
- Export citation
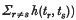 ) is necessary.
) is necessary.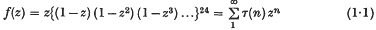
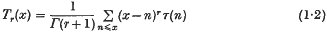



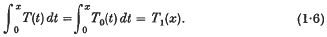
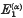 of
of 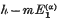 tends to
tends to