Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
The production of 8Li by bombardment of boron with neutrons
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 304-308
- Print publication:
- April 1939
-
- Article
- Export citation
The γ-rays of ionium
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 322-326
- Print publication:
- April 1939
-
- Article
- Export citation
On the stability of nuclei against β-emission
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 242-255
- Print publication:
- April 1939
-
- Article
- Export citation
A peculiarity in the infra-red absorption spectrum of germane
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 341-342
- Print publication:
- April 1939
-
- Article
- Export citation
The heating of iron ammonium alum by alternating magnetic fields at very low temperatures
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 327-335
- Print publication:
- April 1939
-
- Article
- Export citation
Base conditions and covariant systems in an algebraic threefold
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 166-179
- Print publication:
- April 1939
-
- Article
- Export citation
On the easier Waring problem for powers of primes. II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 149-165
- Print publication:
- April 1939
-
- Article
- Export citation
A note on the boundary layer equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 338-340
- Print publication:
- April 1939
-
- Article
- Export citation
A new proof of the joint product moment distribution
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 336-338
- Print publication:
- April 1939
-
- Article
- Export citation
The number of configurations in an assembly and cooperative phenomena
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 265-292
- Print publication:
- April 1939
-
- Article
- Export citation
On the number of real roots of a random algebraic equation. II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 133-148
- Print publication:
- April 1939
-
- Article
- Export citation
PSP volume 35 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- April 1939
-
- Article
-
- You have access
- Export citation
Electronic states at the surfaces of crystals: II. The approximation of tight binding: finite linear chain of atoms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 221-231
- Print publication:
- April 1939
-
- Article
- Export citation
The disintegration of the separated isotopes of boron under proton and deuteron bombardment
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 298-303
- Print publication:
- April 1939
-
- Article
- Export citation
Electronic states at the surfaces of crystals: I. The approximation of nearly free electrons
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 205-220
- Print publication:
- April 1939
-
- Article
- Export citation
Lorentz-invariance in quantum theory
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 186-194
- Print publication:
- April 1939
-
- Article
- Export citation
Time effects in the magnetic cooling method
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 256-264
- Print publication:
- April 1939
-
- Article
- Export citation
Methods of construction of Geiger-Mueller counters and their use in coincidence experiments
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 309-321
- Print publication:
- April 1939
-
- Article
- Export citation
The uncertainty of the reference frame in quantum mechanics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 195-204
- Print publication:
- April 1939
-
- Article
- Export citation
The application of statistical methods to immobile adsorbed films
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 293-297
- Print publication:
- April 1939
-
- Article
- Export citation
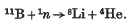
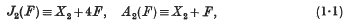
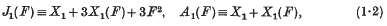
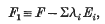
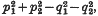 where the letters
where the letters