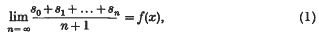Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
Contributions to the theory of Ramanujan's function τ(n) and similar arithmetical functions: I. The zeros of the function
on the line
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 351-356
- Print publication:
- July 1939
-
- Article
- Export citation
Elastic collisions of mesons with electrons and protons
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 463-473
- Print publication:
- July 1939
-
- Article
- Export citation
Quantum electrodynamics. I
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 419-437
- Print publication:
- July 1939
-
- Article
- Export citation
On circles determined by five lines in a plane
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 518-519
- Print publication:
- July 1939
-
- Article
- Export citation
Note on the sensitive time of a Wilson expansion chamber
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 512-515
- Print publication:
- July 1939
-
- Article
- Export citation
Contributions to the theory of Ramanujan's function τ(n) and similar arithmetical functions: II. The order of the Fourier coefficients of integral modular forms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 357-372
- Print publication:
- July 1939
-
- Article
- Export citation
A remark on a theorem of severi
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 516-517
- Print publication:
- July 1939
-
- Article
- Export citation
A note on functions regular and bounded in the unit circle and small at a set of points near the circumference of the circle
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 382-388
- Print publication:
- July 1939
-
- Article
- Export citation
The half-value period of
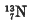
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 523-525
- Print publication:
- July 1939
-
- Article
- Export citation
PSP volume 35 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- July 1939
-
- Article
-
- You have access
- Export citation
PSP volume 35 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- July 1939
-
- Article
-
- You have access
- Export citation
An automatic curve follower for use with the differential analyser
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 494-505
- Print publication:
- July 1939
-
- Article
- Export citation
A new notation for quantum mechanics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 416-418
- Print publication:
- July 1939
-
- Article
- Export citation
On the derivation of discontinuous functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 373-381
- Print publication:
- July 1939
-
- Article
- Export citation
The minimum χ′2 approximation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, p. 520
- Print publication:
- July 1939
-
- Article
- Export citation
Zur Summabilitätstheorie der Fourierschen Doppelreihe
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 343-350
- Print publication:
- July 1939
-
- Article
- Export citation
Quantum electrodynamics. II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 438-462
- Print publication:
- July 1939
-
- Article
- Export citation
A problem in conduction of heat
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 394-404
- Print publication:
- July 1939
-
- Article
- Export citation
The effect of interstellar matter on climatic variation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 405-415
- Print publication:
- July 1939
-
- Article
- Export citation
Note on the calculation of the Peltier effect
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 521-522
- Print publication:
- July 1939
-
- Article
- Export citation
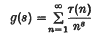
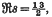 and (2) that of finding an asymptotic formula
and (2) that of finding an asymptotic formula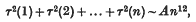
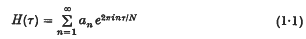
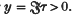 Then
Then