In a previous piece of work(1) numerous data were obtained on the dependence upon magnetizing field of the Benedicks e.m.f. in nickel wire. The work was restricted to a study of the effect of the initial increase of magnetizing field, no hysteresis loops being examined. The curves were most remarkable in that the change of e.m.f. depended upon the direction of the magnetizing field with respect to the temperature asymmetry. In the paper quoted, it was suggested that the curves should be resolved into two components, symmetrical and anti-symmetrical with respect to the field. In the present paper the former component is termed the normal component, because, as is shown later, a simple explanation of it can be given at once. We call the antisymmetrical component the anomalous effect.

In a paper published in the Proceedings of the London Mathematical Society, (2), 40 (1936), 143, Welchman introduced the idea of fundamental scrolls from which all special scrolls may be obtained by projection, and he developed the theory of fundamental line scrolls. These fundamental line scrolls are generated by joins of pairs of corresponding points in a cyclic (1, 1) correspondence of period 2 on a canonical curve. In this paper I generalize some of Welchman's results, and then go on to consider certain fundamental scrolls which have a particular interest.

The foregoing paper by Dr Atkinson relates to the new formula for the rate of accretion of mass by a star that has recently been proposed by us. The derivation of this formula was made by means of a dynamical argument, certain physical aspects having to be neglected.

In a previous paper a new method, based on Kemmer's β-formalism, of calculating meson processes was given for the case in which the meson interacts with an electromagnetic field. This method is now extended to the nuclear interaction, so that the whole of the meson theory can be given either in tensor or in matrix form, the former being preferable when the wave aspect of the meson is important and the latter when the particle aspect is dominant.

As examples of the matrix method, derivations are given of the cross-sections for the nuclear scattering of mesons and for the production of mesons from nuclei by photons. It is pointed out that the usual non-relativistic theory of the nuclear interaction is inadequate even for very small velocities.

In this paper we consider the slow two-dimensional motion of viscous liquid past a sharp edge projecting into the stream, the motion being one of uniform shear apart from the disturbance caused by the projection. A special form is assumed for the boundary so that a method lately developed by N. Muschelišvili can be used in solving the biharmonic equation; a simple expression in finite terms is found for the stream function ψ1. Fig. 1 shows the section ABC of the fixed boundary of the liquid, the equation of the curve ABC is given in § 2, and ψ1 in § 3.

It is shown that the usual molecular orbital treatment for the mobile electrons in unsaturated hydrocarbon molecules is not always satisfactory, since it does not yield a self-consistent field. The conditions under which the field is self-consistent are analysed, and are shown to be satisfied in many cases.

The stability of lattices is discussed from the standpoint of the method of small vibrations. It is shown that it is not necessary to determine the whole vibrational spectrum, but only its long wave part. The stability conditions are nothing but the positive definiteness of the macroscopic deformation energy, and can be expressed in the form of inequalities for the elastic constants. A new method is explained for calculating these as lattice sums, and this method is applied to the three monatomic lattice types assuming central forces. In this way one obtains a simple explanation of the fact that the face-centred lattice is stable, whereas the simple lattice is always unstable and the body-centred also except for small exponents of the attractive forces. It is indicated that this method might be used for an improvement of the, at present, rather unsatisfactory theory of strength.

The transition 20F → 20Ne is shown to occur with the emission of a β-particle of maximum energy 5·0 × 106e. V., followed by a γ-quantum of energy 2·2 × 106e.V.

The transition from the excitation level of 20Ne at 2·2 × 106 e.V. sometimes occurs in two stages with the emission of two quanta of smaller energy.

1. Let r(n) be the number of representations of n as a sum of two squares, d(n) the number of divisors of n, and

where γ is Euler's constant. Thus P(x) is the error term in the problem of the lattice points of a circle, and Δ(x) the error term in Dirichlet's divisor problem, or the problem of the lattice points of a rectangular hyperbola.

The paper describes a method of integrating differential equations by means of the Mallock linear equation machine. The method, which is based on one described by Hartree, is applicable to pairs of second order simultaneous linear ordinary differential equations in two unknowns. Any required degree of accuracy in the solution can be obtained.

1. Any number x can be expressed uniquely in the form

where the xr's are positive integers and where xr < r. In the present paper we consider the set of numbers Eb for which the xr's are bounded, so that 0 ≤ xr < b say, where b also is an integer. We prove that this set has dimension function

h(t) = b−u,

where t = euu−u−½(b − 1)(2π)−½, in the sense of Hausdorff.

The penetrating component of cosmic radiation is now believed to consist of mesons—particles with a mass about one-tenth of that of a proton—while the soft component is attributed to electrons. By collisions with atomic electrons a fast meson occasionally produces fast secondary electrons, “knock-on” electrons, thus giving rise to a certain amount of the soft component. It was first suggested by Bhabha(1) that fast electrons produced in this way may be responsible for the electron showers known to be associated with the penetrating particles. In the present note we calculate the ratio, which we denote by R, of the average number of electrons which accompany a meson due to the knock-on process, making use of the simplification which results from the fact that the rate of loss of energy by fast electrons in ionization and excitation and also the emission of soft quanta are nearly independent of their energy. In virtue of this, the total length of electron track, and therefore the magnitude of R, is only slightly affected by the cascade process of shower production, a process which causes the energy of a fast electron to be shared among a number of electrons. The difficulties associated with a treatment of the cascade process may therefore be avoided in calculating R.

It frequently happens that we wish to evaluate the total energy of the mobile, or π, electrons in an unsaturated hydrocarbon molecule. According to the method of molecular orbitals(1) this energy is the sum of individual electronic energies ∊r, and the summation is over all the occupied orbitals. The energies ∊r are the roots of the secular determinant, and, if we write

and suppose that there are n unsaturated carbon atoms, then the equation that gives the energies zr is

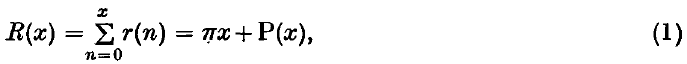
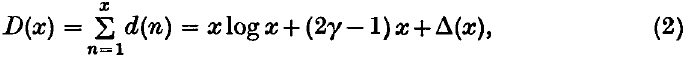
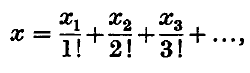
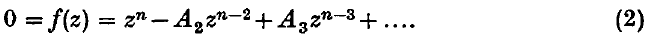
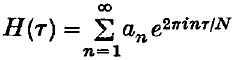Suppose that is an integral modular form of dimensions − κ, where κ > 0, and 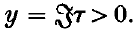Stufe N, which vanishes at all the rational cusps of the fundamental region, and which is absolutely convergent for The purpose of this note is to prove that

The notation employed is that of my second paper under the same general title* I refer to this paper as II.

The unusual physical properties of liquid He ii have led to considerable speculation concerning its internal structure. Since the entropy difference between the liquid and solid states tends to zero as the temperature approaches absolute zero, it appears that in the neighbourhood of zero temperature the liquid must have some kind of ordered structure, and London's theoretical investigations(1) indicated that the best agreement could be obtained with the observed energy and molecular volume by supposing the liquid to have a diamond lattice. On the basis of this work Fröhlich(2) then suggested that in the ordered state He ii possessed a diamond lattice, and that the disordering process consisted in an interchange of the atoms between this lattice and the vacant points of the body-centred cubic lattice from which the diamond lattice may be considered as derived.