Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
Note on a Divergent Series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 1 / January 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-8
- Print publication:
- January 1941
-
- Article
- Export citation
Some Properties of Quaternary Alloy Equilibrium Diagrams
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 1 / January 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 95-101
- Print publication:
- January 1941
-
- Article
- Export citation
Generalized Helices in an Ordinary Vn
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 1 / January 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 14-28
- Print publication:
- January 1941
-
- Article
- Export citation
The Stability of Crystal Lattices: V. Experimental Evidence on Recent Theories of the Equation of State and the Melting of Solids
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 1 / January 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 34-54
- Print publication:
- January 1941
-
- Article
- Export citation
On Frullani Integrals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 1 / January 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 9-13
- Print publication:
- January 1941
-
- Article
- Export citation
Momentum Distribution in Molecular Systems: Part II. Carbon and the C—H Bond
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 1 / January 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 67-73
- Print publication:
- January 1941
-
- Article
- Export citation
PSP volume 37 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 1 / January 1941
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- January 1941
-
- Article
-
- You have access
- Export citation
Momentum Distribution in Molecular Systems: Part III. Bonds of Higher Order
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 1 / January 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 74-81
- Print publication:
- January 1941
-
- Article
- Export citation
The Theory of Adsorption of Gases on Solids when the Potential Energy Varies Continuously over the Surface
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 1 / January 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 82-94
- Print publication:
- January 1941
-
- Article
- Export citation
PSP volume 37 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 1 / January 1941
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
- Print publication:
- January 1941
-
- Article
-
- You have access
- Export citation
The Characteristic Exponents of a Pair of Power Series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 1 / January 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 105-108
- Print publication:
- January 1941
-
- Article
- Export citation
Momentum Distribution in Molecular Systems: Part I. The Single Bond
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 1 / January 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 55-66
- Print publication:
- January 1941
-
- Article
- Export citation
Note on General Bi-Harmonic Analysis for a Plate Containing Circular Holes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 1 / January 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 29-33
- Print publication:
- January 1941
-
- Article
- Export citation
The electrostatic dipole moment of a nucleus in the meson theory
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 36 / Issue 4 / October 1940
- Published online by Cambridge University Press:
- 24 October 2008, pp. 438-440
- Print publication:
- October 1940
-
- Article
- Export citation
Proceedings at the meetings held during the session 1939–1940: Annual General Meeting
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 36 / Issue 4 / October 1940
- Published online by Cambridge University Press:
- 24 October 2008, pp. 511-512
- Print publication:
- October 1940
-
- Article
- Export citation
Deuteron bombardment of silver
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 36 / Issue 4 / October 1940
- Published online by Cambridge University Press:
- 24 October 2008, pp. 500-506
- Print publication:
- October 1940
-
- Article
- Export citation
PSP volume 36 issue 4 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 36 / Issue 4 / October 1940
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b9
- Print publication:
- October 1940
-
- Article
-
- You have access
- Export citation
On semi-groups
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 36 / Issue 4 / October 1940
- Published online by Cambridge University Press:
- 24 October 2008, pp. 387-400
- Print publication:
- October 1940
-
- Article
- Export citation
A note on Morley's trisector theorem
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 36 / Issue 4 / October 1940
- Published online by Cambridge University Press:
- 24 October 2008, pp. 401-413
- Print publication:
- October 1940
-
- Article
- Export citation
Rough measurement of high viscosities
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 36 / Issue 4 / October 1940
- Published online by Cambridge University Press:
- 24 October 2008, pp. 507-508
- Print publication:
- October 1940
-
- Article
- Export citation

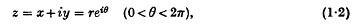

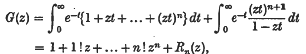
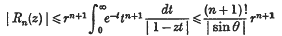
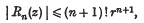
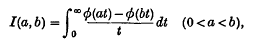
 and H
and H