Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
On Hausdorff's methods of summability
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 166-192
- Print publication:
- April 1942
-
- Article
- Export citation
On the determination of intermolecular energies by inductive analysis
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 224-230
- Print publication:
- April 1942
-
- Article
- Export citation
Some relations between certain methods of summation of infinite series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 144-164
- Print publication:
- April 1942
-
- Article
- Export citation
A note on k-connexes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 129-143
- Print publication:
- April 1942
-
- Article
- Export citation
Two-centre integrals occurring in the theory of molecular structure
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 210-223
- Print publication:
- April 1942
-
- Article
- Export citation
On Lorentz invariance in the quantum theory. II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 201-209
- Print publication:
- April 1942
-
- Article
- Export citation
Relations between concentrated sets and sets possessing property C
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 20-23
- Print publication:
- January 1942
-
- Article
- Export citation
On the stability of crystal lattices IX. Covariant theory of lattice deformations and the stability of some hexagonal lattices
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 82-99
- Print publication:
- January 1942
-
- Article
- Export citation
PSP volume 38 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- January 1942
-
- Article
-
- You have access
- Export citation
A theorem on s-dimensional measure of sets of points
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 24-27
- Print publication:
- January 1942
-
- Article
- Export citation
On the stability of crystal lattices VIII. Stability of rhombohedral Bravais lattices*
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 67-81
- Print publication:
- January 1942
-
- Article
- Export citation
Expansions for a particular class of exponential-logarithmic integrals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 34-39
- Print publication:
- January 1942
-
- Article
- Export citation
On certain expansions of the solutions of Mathieu'S differential equation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 28-33
- Print publication:
- January 1942
-
- Article
- Export citation
Initial stress and elastic instability
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 125-128
- Print publication:
- January 1942
-
- Article
- Export citation
On the Parseval formulae for Fourier transforms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-19
- Print publication:
- January 1942
-
- Article
- Export citation
Momentum distribution in molecular systems. Part VI. Shape of the Compton line for methane CH4
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 100-108
- Print publication:
- January 1942
-
- Article
- Export citation
PSP volume 38 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- January 1942
-
- Article
-
- You have access
- Export citation
The number of configurations of a cooperative assembly
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 109-124
- Print publication:
- January 1942
-
- Article
- Export citation
On the stability of crystal lattices VII. Long-wave and short-wave stability for the face-centred cubic lattice
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 61-66
- Print publication:
- January 1942
-
- Article
- Export citation
Relativistic dynamics of a spinning magnetic particle
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 40-60
- Print publication:
- January 1942
-
- Article
- Export citation
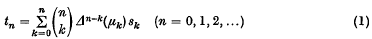
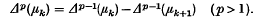


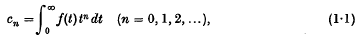
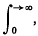 or possibly
or possibly 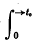 if
if 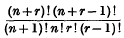
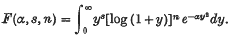
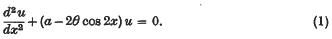



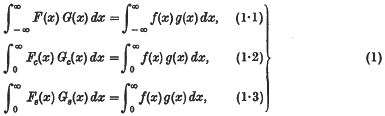
 and
and  For molecules which occupy three sites on the lattice the corresponding results are
For molecules which occupy three sites on the lattice the corresponding results are  and
and  when the molecules are perfectly flexible and
when the molecules are perfectly flexible and  and
and  when the molecules are completely inflexible,
when the molecules are completely inflexible, 