Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
The thermodynamics of crystal lattices: I. Discussion of the methods of calculation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 2 / June 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 100-103
- Print publication:
- June 1943
-
- Article
- Export citation
The thermodynamics of crystal lattices: II. Calculation of certain lattice sums occurring in thermodynamics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 2 / June 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 104-113
- Print publication:
- June 1943
-
- Article
- Export citation
The Vapour-Pressure Equations of Solutions and the Osmotic Pressure of Rubber
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 1 / March 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 54-67
- Print publication:
- March 1943
-
- Article
- Export citation
The Fixed Part of the Canonical System
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 1 / March 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 31-34
- Print publication:
- March 1943
-
- Article
- Export citation
On the Product of Three Homogeneous Linear Forms. IV
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 1 / March 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-21
- Print publication:
- March 1943
-
- Article
- Export citation
PSP volume 39 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 1 / March 1943
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
- Print publication:
- March 1943
-
- Article
- Export citation
PSP volume 39 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 1 / March 1943
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- March 1943
-
- Article
- Export citation
Bases for the Prime Ideals Associated with Certain Classes of Algebraic Varieties
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 1 / March 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 35-48
- Print publication:
- March 1943
-
- Article
- Export citation
Some Enumerative Results in the Theory of Forms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 1 / March 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 22-30
- Print publication:
- March 1943
-
- Article
- Export citation
The Measure of Plane Sets
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 1 / March 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 51-53
- Print publication:
- March 1943
-
- Article
- Export citation
On Pulses whose Travel Times are not True Minima
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 1 / March 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 48-51
- Print publication:
- March 1943
-
- Article
- Export citation
Note on a Paper ‘On the Theory of Successive Radioactive Transformations’*
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 1 / March 1943
- Published online by Cambridge University Press:
- 24 October 2008, p. 68
- Print publication:
- March 1943
-
- Article
- Export citation
On Hausdorff's methods of summability. II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 4 / November 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 344-363
- Print publication:
- November 1942
-
- Article
- Export citation
Proceedings at the meetings held during the session 1941–1942: Annual General Meeting
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 4 / November 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 406-407
- Print publication:
- November 1942
-
- Article
- Export citation
Some generalizations of the ergodic theorem
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 4 / November 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 325-343
- Print publication:
- November 1942
-
- Article
- Export citation
PSP volume 38 issue 4 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 4 / November 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b9
- Print publication:
- November 1942
-
- Article
-
- You have access
- Export citation
Note on a limit related to the curvatures of two surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 4 / November 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 399-400
- Print publication:
- November 1942
-
- Article
- Export citation
An inequality for two triangles
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 4 / November 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 397-398
- Print publication:
- November 1942
-
- Article
- Export citation
On the number of terms in a simple algebraic form
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 4 / November 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 394-396
- Print publication:
- November 1942
-
- Article
- Export citation
PSP volume 38 issue 4 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 4 / November 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- November 1942
-
- Article
-
- You have access
- Export citation
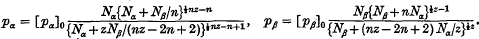
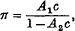
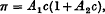
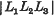

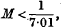
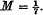 If we denote by θ, ø, ψ the roots of the cubic equation
If we denote by θ, ø, ψ the roots of the cubic equation 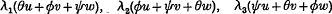
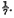 In this case, L
In this case, L
 where
where 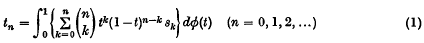
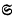 denotes a set of elements
denotes a set of elements 
