Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
On lattice points in the domain |xy | ≤1, | x + y | ≤√5, and applications to asymptotic formulae in lattice point theory (II)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 2 / June 1944
- Published online by Cambridge University Press:
- 24 October 2008, pp. 116-120
- Print publication:
- June 1944
-
- Article
- Export citation
PSP volume 40 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 2 / June 1944
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- June 1944
-
- Article
- Export citation
On lattice points in the domain |xy| ≤1, | x+y| ≤ √5, and applications to asymptotic formulae in lattice point theory (I)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 2 / June 1944
- Published online by Cambridge University Press:
- 24 October 2008, pp. 107-116
- Print publication:
- June 1944
-
- Article
- Export citation
The effect of a hole on certain stress distributions in aeolotropic and isotropic plates
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 2 / June 1944
- Published online by Cambridge University Press:
- 24 October 2008, pp. 172-188
- Print publication:
- June 1944
-
- Article
- Export citation
On the quartic surface

-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 2 / June 1944
- Published online by Cambridge University Press:
- 24 October 2008, pp. 121-145
- Print publication:
- June 1944
-
- Article
- Export citation
The thermodynamics of crystal lattices: IV. The elastic constants of a face-centred cubic lattice with central forces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 2 / June 1944
- Published online by Cambridge University Press:
- 24 October 2008, pp. 151-166
- Print publication:
- June 1944
-
- Article
- Export citation
A theorem on finite differences with an application to the theory of Hausdorff summability
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 2 / June 1944
- Published online by Cambridge University Press:
- 24 October 2008, pp. 188-196
- Print publication:
- June 1944
-
- Article
- Export citation
PSP volume 40 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 2 / June 1944
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- June 1944
-
- Article
- Export citation
Scattering of charged mesons under the influence of radiation damping
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 2 / June 1944
- Published online by Cambridge University Press:
- 24 October 2008, pp. 167-172
- Print publication:
- June 1944
-
- Article
- Export citation
Note on the theory of series (XXIII): On the partial sums of Fourier series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 2 / June 1944
- Published online by Cambridge University Press:
- 24 October 2008, pp. 103-107
- Print publication:
- June 1944
-
- Article
- Export citation
PSP volume 40 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 1 / March 1944
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- March 1944
-
- Article
- Export citation
The ionization method of measuring neutron energy
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 1 / March 1944
- Published online by Cambridge University Press:
- 24 October 2008, pp. 72-102
- Print publication:
- March 1944
-
- Article
- Export citation
Absorption and coincidence experiments with 198Au
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 1 / March 1944
- Published online by Cambridge University Press:
- 24 October 2008, pp. 57-71
- Print publication:
- March 1944
-
- Article
- Export citation
The geometry of the binary quintic form
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 1 / March 1944
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-5
- Print publication:
- March 1944
-
- Article
- Export citation
PSP volume 40 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 1 / March 1944
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- March 1944
-
- Article
- Export citation
On the shearing motion of fluid past a projection
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 1 / March 1944
- Published online by Cambridge University Press:
- 24 October 2008, pp. 19-36
- Print publication:
- March 1944
-
- Article
- Export citation
A type of stress distribution on the surface of a semi-infinite elastic solid
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 1 / March 1944
- Published online by Cambridge University Press:
- 24 October 2008, pp. 5-19
- Print publication:
- March 1944
-
- Article
- Export citation
The evaluation of the cosmical number
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 40 / Issue 1 / March 1944
- Published online by Cambridge University Press:
- 24 October 2008, pp. 37-56
- Print publication:
- March 1944
-
- Article
- Export citation
A relativistic formula for the scattering of mesons under the influence of radiation damping
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 3 / October 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 168-172
- Print publication:
- October 1943
-
- Article
- Export citation
Momentum distribution in molecular systems: Part VII. Momentum distribution and shape of the Compton line for Li2 and N2
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 3 / October 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 180-188
- Print publication:
- October 1943
-
- Article
- Export citation







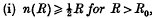
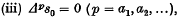
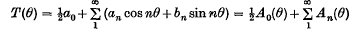
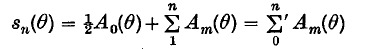
 . 136 . 2
. 136 . 2