Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
Note additionnelle à l'article ‘La théorie des noyaux reproduisants et ses applications’
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 3 / October 1943
- Published online by Cambridge University Press:
- 24 October 2008, p. 205
- Print publication:
- October 1943
-
- Article
- Export citation
La théorie des noyaux reproduisants et ses applications Première Partie
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 3 / October 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 133-153
- Print publication:
- October 1943
-
- Article
- Export citation
Some manifolds generated by normal rational curves
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 3 / October 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 153-159
- Print publication:
- October 1943
-
- Article
- Export citation
On the number of terms in a simple algebraic form under the symplectic group
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 3 / October 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 197-199
- Print publication:
- October 1943
-
- Article
- Export citation
The Cambridge Philosophical Society Statement of Accounts for the Period 1 August 1941 to 31 July 1942
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 3 / October 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 207-208
- Print publication:
- October 1943
-
- Article
- Export citation
PSP volume 39 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 3 / October 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- October 1943
-
- Article
-
- You have access
- Export citation
The algebra of meson matrices
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 3 / October 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 189-196
- Print publication:
- October 1943
-
- Article
- Export citation
A problem in the summation of series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 3 / October 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 200-202
- Print publication:
- October 1943
-
- Article
- Export citation
The focal form of the quadric in n dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 3 / October 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 159-167
- Print publication:
- October 1943
-
- Article
- Export citation
The hydrogen atom and the classical theory of radiation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 3 / October 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 173-180
- Print publication:
- October 1943
-
- Article
- Export citation
PSP volume 39 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 3 / October 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b7
- Print publication:
- October 1943
-
- Article
-
- You have access
- Export citation
Statistical mechanics of dimerization in perfect solutions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 3 / October 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 202-204
- Print publication:
- October 1943
-
- Article
- Export citation
Proceedings at the Meetings held during the Session 1942–1943: Annual general meeting
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 3 / October 1943
- Published online by Cambridge University Press:
- 24 October 2008, p. 206
- Print publication:
- October 1943
-
- Article
- Export citation
PSP volume 39 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 2 / June 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- June 1943
-
- Article
-
- You have access
- Export citation
The energy loss by radiation of fast electrons in a Coulomb field
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 2 / June 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 127-130
- Print publication:
- June 1943
-
- Article
- Export citation
The thermodynamics of crystal lattices: III. The equation of state for a face-centred cubic lattice
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 2 / June 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 113-127
- Print publication:
- June 1943
-
- Article
- Export citation
On the statistics of random distributions of paired events, with applications to the results obtained in the use of the interval selector with particle counters
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 2 / June 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 84-99
- Print publication:
- June 1943
-
- Article
- Export citation
The vapour pressure equation of solutions and the osmotic pressure of rubber*
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 2 / June 1943
- Published online by Cambridge University Press:
- 24 October 2008, p. 131
- Print publication:
- June 1943
-
- Article
-
- You have access
- Export citation
Stratified systems of logic
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 2 / June 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. 69-83
- Print publication:
- June 1943
-
- Article
- Export citation
PSP volume 39 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 39 / Issue 2 / June 1943
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- June 1943
-
- Article
-
- You have access
- Export citation
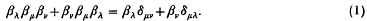
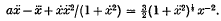
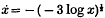 . Thus a collision is possible for like charges and not possible for unlike charges. The result, in both cases, is the opposite of what we should expect from elementary physical considerations.
. Thus a collision is possible for like charges and not possible for unlike charges. The result, in both cases, is the opposite of what we should expect from elementary physical considerations.