Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
Relativistic wave equations for zero rest-mass
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 1 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 49-56
- Print publication:
- June 1945
-
- Article
- Export citation
The energy levels of ‘holes’ in liquids
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 2 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 180-183
- Print publication:
- June 1945
-
- Article
- Export citation
The symmetrical vibrations of a thin elastic plate
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 1 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 27-43
- Print publication:
- June 1945
-
- Article
- Export citation
On the representations of a number as a sum of squares and certain related identities
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 1 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-11
- Print publication:
- June 1945
-
- Article
- Export citation
On the classical theory of radiating electrons
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 2 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 184-186
- Print publication:
- June 1945
-
- Article
- Export citation
Expansions of coordinates of points of a plane curve in terms of s or Ψ
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 1 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 68-70
- Print publication:
- June 1945
-
- Article
- Export citation
The ‘odd’ number six
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 1 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 66-68
- Print publication:
- June 1945
-
- Article
- Export citation
Negative probability
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 1 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 71-73
- Print publication:
- June 1945
-
- Article
- Export citation
The minima of a pair of indefinite, harmonic, binary quadratic forms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 2 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 77-96
- Print publication:
- June 1945
-
- Article
- Export citation
The dynamics of a simple system. I. Observables
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 1 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 57-65
- Print publication:
- June 1945
-
- Article
- Export citation
An extension of a theorem of Mehler's on Hermite polynomials
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 1 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 12-15
- Print publication:
- June 1945
-
- Article
- Export citation
Conduction of heat in a slab in contact with well-stirred fluid
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 1 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-49
- Print publication:
- June 1945
-
- Article
- Export citation
On multiple curves. II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 2 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 117-126
- Print publication:
- June 1945
-
- Article
- Export citation
On the summation of certain trigonometric series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 2 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 145-160
- Print publication:
- June 1945
-
- Article
- Export citation
PSP volume 41 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 1 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- June 1945
-
- Article
-
- You have access
- Export citation
On multiple curves. I
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 2 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-117
- Print publication:
- June 1945
-
- Article
- Export citation
A method for computing the resonant wave-length of a type of cavity resonator
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 2 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 160-175
- Print publication:
- June 1945
-
- Article
- Export citation
Note on the equation
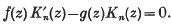
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 1 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 74-75
- Print publication:
- June 1945
-
- Article
- Export citation
Point-curve correspondences: I. The theory of the base
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 2 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 135-145
- Print publication:
- June 1945
-
- Article
- Export citation
A general form of the covering principle and relative differentiation of additive functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 2 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 103-110
- Print publication:
- June 1945
-
- Article
- Export citation
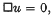 being the relativistic Laplace operator. Analogous questions for any orthogonal group are dealt with in a previous paper, but it was thought that an independent and not too technical treatment for the Lorentz group might be of interest.
being the relativistic Laplace operator. Analogous questions for any orthogonal group are dealt with in a previous paper, but it was thought that an independent and not too technical treatment for the Lorentz group might be of interest.
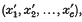 are only considered to be the same solution if
are only considered to be the same solution if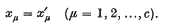
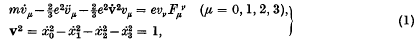
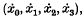 , and the external electromagnetic field is described by the usual field quantities
, and the external electromagnetic field is described by the usual field quantities 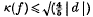 and that this is a ‘best possible’ result.
and that this is a ‘best possible’ result.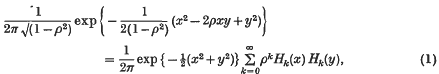
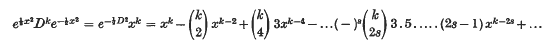
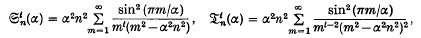
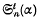 and
and 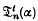 for
for 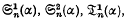
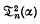 and the series Θ
and the series Θ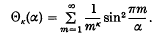
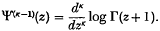 The general expressions for
The general expressions for 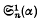 and
and 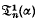 involve Ψ(
involve Ψ(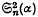 and
and 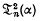 are independent of
are independent of