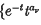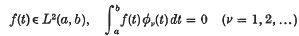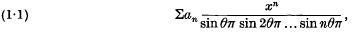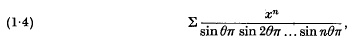Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
Derivation of Dirac's equation for a free particle
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 2 / June 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 185-187
- Print publication:
- June 1946
-
- Article
- Export citation
Intersection groups and rings
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 2 / June 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 183-184
- Print publication:
- June 1946
-
- Article
- Export citation
Collective electron assemblies in a metal with overlapping energy bands: Part I. General theory
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 2 / June 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 139-144
- Print publication:
- June 1946
-
- Article
- Export citation
PSP volume 42 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 2 / June 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- June 1946
-
- Article
-
- You have access
- Export citation
Collective electron assemblies in a metal with overlapping energy bands: Part II. The occurrence of ferromagnetism
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 2 / June 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 144-155
- Print publication:
- June 1946
-
- Article
- Export citation
Approximate methods in surge-tank calculations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 2 / June 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 156-166
- Print publication:
- June 1946
-
- Article
- Export citation
On the closure of
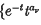
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 2 / June 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 91-105
- Print publication:
- June 1946
-
- Article
- Export citation
PSP volume 42 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 2 / June 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- June 1946
-
- Article
-
- You have access
- Export citation
The combustion of wood. Part I
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 2 / June 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 166-182
- Print publication:
- June 1946
-
- Article
- Export citation
Notes on the theory of series (XXIV): a curious power-series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 2 / June 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 85-90
- Print publication:
- June 1946
-
- Article
- Export citation
Optical characteristics of a two-cylinder electrostatic lens
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 2 / June 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 106-126
- Print publication:
- June 1946
-
- Article
- Export citation
A note on the Hamiltonian equations of motion
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 2 / June 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 132-138
- Print publication:
- June 1946
-
- Article
- Export citation
A note on the Petzval field curvature in electron-optical systems
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 2 / June 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 127-131
- Print publication:
- June 1946
-
- Article
- Export citation
Analysis of operation of a thermostat with contact thermo-regulator
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 1 / February 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 62-72
- Print publication:
- February 1946
-
- Article
- Export citation
On the scattering of fast neutrons by protons*
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 1 / February 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 45-54
- Print publication:
- February 1946
-
- Article
- Export citation
On Mathisson's variational equation of relativistic dynamics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 1 / February 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 54-61
- Print publication:
- February 1946
-
- Article
- Export citation
PSP volume 42 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 1 / February 1946
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
- Print publication:
- February 1946
-
- Article
-
- You have access
- Export citation
A general form of the covering principle and relative differentiation of additive functions. II†
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 1 / February 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-10
- Print publication:
- February 1946
-
- Article
- Export citation
On multiple curves. III.
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 1 / February 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 11-14
- Print publication:
- February 1946
-
- Article
- Export citation
On the characteristic function of the distribution of the product of two normal variates
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 1 / February 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 82-84
- Print publication:
- February 1946
-
- Article
- Export citation