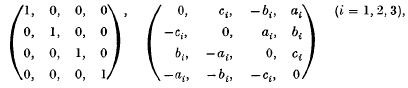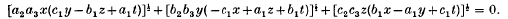Refine search
Actions for selected content:
26205 results in Theoretical Physics and Mathematical Physics
The classical equations of motion of an electron
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 278-286
- Print publication:
- October 1946
-
- Article
- Export citation
The number of configurations of molecules on a lattice
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 303-310
- Print publication:
- October 1946
-
- Article
- Export citation
PSP volume 42 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b5
- Print publication:
- October 1946
-
- Article
-
- You have access
- Export citation
The resultant of a large number of events of random phase
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 245-249
- Print publication:
- October 1946
-
- Article
- Export citation
PSP volume 42 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
- Print publication:
- October 1946
-
- Article
-
- You have access
- Export citation
The elastic stresses produced in a thick plate by the application of pressure to its free surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 260-271
- Print publication:
- October 1946
-
- Article
- Export citation
The elastic response of a large plate to a Gaussian distribution of pressure varying with time
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 338-341
- Print publication:
- October 1946
-
- Article
- Export citation
The complete system of the binary (4, 1) form
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 206-216
- Print publication:
- October 1946
-
- Article
- Export citation
Proceedings at the meetings held during the session 1945–1946: Annual General Meeting
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 342-343
- Print publication:
- October 1946
-
- Article
- Export citation
The cambridge philosophical society statement of accounts for the year ended 31 JULY 1945
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 344-345
- Print publication:
- October 1946
-
- Article
- Export citation
The variation of the dipole moment of adsorbed particles with the fraction of the surface covered*
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 292-303
- Print publication:
- October 1946
-
- Article
- Export citation
A new type of boundary-value problem in hyperbolic equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 250-260
- Print publication:
- October 1946
-
- Article
- Export citation
Statistical mechanics and the partitions of numbers
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 272-277
- Print publication:
- October 1946
-
- Article
- Export citation
Two moment problems for bounded functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 189-196
- Print publication:
- October 1946
-
- Article
- Export citation
The large-sample theory of sequential tests
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 239-244
- Print publication:
- October 1946
-
- Article
- Export citation
On the generation of sets of four tetrahedra of which any two are mutually inscribed
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 217-225
- Print publication:
- October 1946
-
- Article
- Export citation
Note to the preceding paper by C. V. H. Rao
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 226-229
- Print publication:
- October 1946
-
- Article
- Export citation
Diamagnetism and superconductivity of a collective electron assembly
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 311-327
- Print publication:
- October 1946
-
- Article
- Export citation
Point-curve correspondences: II. Induced and extended correspondences
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 229-239
- Print publication:
- October 1946
-
- Article
- Export citation
The complete system of the binary (3, 1) form
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 196-205
- Print publication:
- October 1946
-
- Article
- Export citation


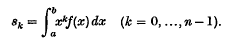
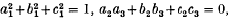 and with a positive determinant, then the four tetrahedra,
and with a positive determinant, then the four tetrahedra,