Refine search
Actions for selected content:
26208 results in Theoretical Physics and Mathematical Physics
Combinants of a pencil of quadric surfaces. II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 4 / October 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 488-490
- Print publication:
- October 1947
-
- Article
- Export citation
Note on the conditions for a p-cycle of an algebraic manifold to be of rank k
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 4 / October 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 577-580
- Print publication:
- October 1947
-
- Article
- Export citation
On the problem of random flights
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 4 / October 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 581-582
- Print publication:
- October 1947
-
- Article
- Export citation
The measurement of double and triple correlation derivatives in isotropic turbulence
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 4 / October 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 560-570
- Print publication:
- October 1947
-
- Article
- Export citation
Combinants of a pencil of quadric surfaces. I
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 4 / October 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 475-487
- Print publication:
- October 1947
-
- Article
- Export citation
Kolmogoroff's theory of locally isotropic turbulence
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 4 / October 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 533-559
- Print publication:
- October 1947
-
- Article
- Export citation
Corrigenda
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 4 / October 1947
- Published online by Cambridge University Press:
- 24 October 2008, p. 590
- Print publication:
- October 1947
-
- Article
-
- You have access
- Export citation
Some remarks on Schottky's theorem
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 4 / October 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 442-454
- Print publication:
- October 1947
-
- Article
- Export citation
On the algebra of the meson matrices
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 3 / July 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 414-421
- Print publication:
- July 1947
-
- Article
- Export citation
Random associations on a lattice
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 3 / July 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 321-328
- Print publication:
- July 1947
-
- Article
- Export citation
The problem of random intervals on a line
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 3 / July 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 329-341
- Print publication:
- July 1947
-
- Article
- Export citation
The effect of a fixed vertical barrier on surface waves in deep water
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 3 / July 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 374-382
- Print publication:
- July 1947
-
- Article
- Export citation
On the integrals of a partial differential equation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 3 / July 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 348-359
- Print publication:
- July 1947
-
- Article
- Export citation
Simple progressive solutions of the wave equation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 3 / July 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 360-373
- Print publication:
- July 1947
-
- Article
- Export citation
Rectilinear plastic flow of a Bingham solid: I. Flow between eccentric circular cylinders in relative motion
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 3 / July 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 396-405
- Print publication:
- July 1947
-
- Article
- Export citation
The Parseval formulae for monotonic functions. I
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 3 / July 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 289-306
- Print publication:
- July 1947
-
- Article
- Export citation
Configurations of closed ring molecules
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 3 / July 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 422-428
- Print publication:
- July 1947
-
- Article
- Export citation
The theory of surfaces in a geometry based on the notion of area
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 3 / July 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 307-313
- Print publication:
- July 1947
-
- Article
- Export citation
Two-dimensional plastic flow of a Bingham solid: A plastic boundary-layer theory for slow motion
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 3 / July 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 383-395
- Print publication:
- July 1947
-
- Article
- Export citation
The distribution of projected areas of fragments
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 3 / July 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 342-347
- Print publication:
- July 1947
-
- Article
- Export citation
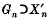 .
.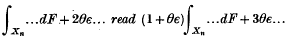 .
.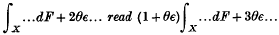 .
.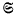 the class of all functions regular in |
the class of all functions regular in |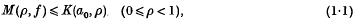


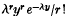 (see e.g. (1)). Consider the case when each event consists of an interval of length α (an event being characterized by its first point). What is the probability that the covered portion of the interval [0,
(see e.g. (1)). Consider the case when each event consists of an interval of length α (an event being characterized by its first point). What is the probability that the covered portion of the interval [0, 
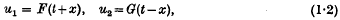

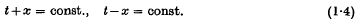
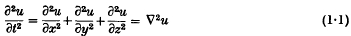
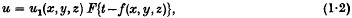
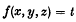
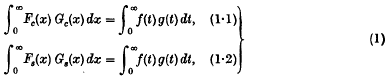
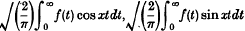 respectively; and
respectively; and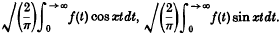 .
.

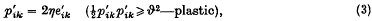

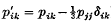 ). The dilatation is denoted by Δ. The rigidity and bulk moduli μ and κ are, if not constants, essentially scalar functions of the stress tensor. The variable viscosity η involves two constants, the yield value ϑ and the reciprocal mobility η
). The dilatation is denoted by Δ. The rigidity and bulk moduli μ and κ are, if not constants, essentially scalar functions of the stress tensor. The variable viscosity η involves two constants, the yield value ϑ and the reciprocal mobility η