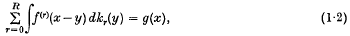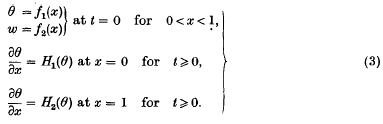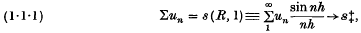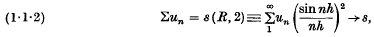Refine search
Actions for selected content:
26205 results in Theoretical Physics and Mathematical Physics
On a class of linear integro-differential equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 2 / April 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 153-163
- Print publication:
- April 1947
-
- Article
- Export citation
A variational method for determining eigenvalues of the wave equation applied to tropospheric refraction*
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 2 / April 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 213-219
- Print publication:
- April 1947
-
- Article
- Export citation
Waves on the surface of a compressible liquid
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 75-95
- Print publication:
- January 1947
-
- Article
- Export citation
A note on Talbot's bands
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 130-133
- Print publication:
- January 1947
-
- Article
- Export citation
A note on white light fringes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 134-136
- Print publication:
- January 1947
-
- Article
- Export citation
A ring in graph theory
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 26-40
- Print publication:
- January 1947
-
- Article
- Export citation
A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 50-67
- Print publication:
- January 1947
-
- Article
- Export citation
PSP volume 43 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- January 1947
-
- Article
-
- You have access
- Export citation
Integral modular forms and summation formulae
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 127-129
- Print publication:
- January 1947
-
- Article
- Export citation
A note on the distribution of the different orderings of n objects
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-9
- Print publication:
- January 1947
-
- Article
- Export citation
Time effects in the magnetic cooling method. II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 118-122
- Print publication:
- January 1947
-
- Article
- Export citation
Notes on Fourier series (IV): Summability (R2)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 10-25
- Print publication:
- January 1947
-
- Article
- Export citation
The flexure and torsion of aeolotropic beams
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 68-74
- Print publication:
- January 1947
-
- Article
- Export citation
A rational formulation of the equations of plastic flow for a Bingham solid
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 100-105
- Print publication:
- January 1947
-
- Article
- Export citation
Note on waves on the surface of running water
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 96-99
- Print publication:
- January 1947
-
- Article
- Export citation
Excitation of indium 113 by X-rays†
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 123-126
- Print publication:
- January 1947
-
- Article
- Export citation
On the theory of spinning particles
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 106-117
- Print publication:
- January 1947
-
- Article
- Export citation
PSP volume 43 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
- Print publication:
- January 1947
-
- Article
-
- You have access
- Export citation
Functions of a statistical variate with given means, with special reference to Laplacian distributions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 43 / Issue 1 / January 1947
- Published online by Cambridge University Press:
- 24 October 2008, pp. 41-49
- Print publication:
- January 1947
-
- Article
- Export citation
A theory of the critical temperatures of the normal paraffins
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 3 / October 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 328-337
- Print publication:
- October 1946
-
- Article
- Export citation