Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
Additive functions of intervals and Hausdorff measure
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 1 / February 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 15-23
- Print publication:
- February 1946
-
- Article
- Export citation
On the variation of visual acuity with light intensity
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 1 / February 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 78-82
- Print publication:
- February 1946
-
- Article
- Export citation
An explanation of anomalous thermionic emission current constants
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 1 / February 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 72-77
- Print publication:
- February 1946
-
- Article
- Export citation
Boussinesq's problem for a flat-ended cylinder
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 1 / February 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 29-39
- Print publication:
- February 1946
-
- Article
- Export citation
On some cases of the reflexion of surface waves by an inclined plane barrier
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 1 / February 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 24-28
- Print publication:
- February 1946
-
- Article
- Export citation
PSP volume 42 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 1 / February 1946
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- February 1946
-
- Article
-
- You have access
- Export citation
Radiating electron in a magnetic field
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 42 / Issue 1 / February 1946
- Published online by Cambridge University Press:
- 24 October 2008, pp. 40-44
- Print publication:
- February 1946
-
- Article
- Export citation
Projective collineations in a space of k-spreads
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 3 / November 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 210-223
- Print publication:
- November 1945
-
- Article
- Export citation
PSP volume 41 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 3 / November 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b6
- Print publication:
- November 1945
-
- Article
-
- You have access
- Export citation
The Cambridge Philosophical Society Statement of Accounts for the Year Ended 31 July 1944: General Account
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 3 / November 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 248-249
- Print publication:
- November 1945
-
- Article
- Export citation
The Fourier transform solution of an elastic wave equation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 3 / November 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 239-243
- Print publication:
- November 1945
-
- Article
- Export citation
On the reflexion of surface waves by a submerged plane barrier
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 3 / November 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 231-238
- Print publication:
- November 1945
-
- Article
- Export citation
Proceedings at the meetings held during the session 1944–1945: Annual General Meeting
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 3 / November 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 244-247
- Print publication:
- November 1945
-
- Article
- Export citation
The biaxial surfaces, and the equivalence of binary forms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 3 / November 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 187-209
- Print publication:
- November 1945
-
- Article
- Export citation
A note on certain stress distributions in isotropic and aeolotropic materials
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 3 / November 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 224-231
- Print publication:
- November 1945
-
- Article
- Export citation
PSP volume 41 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 3 / November 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- November 1945
-
- Article
-
- You have access
- Export citation
PSP volume 41 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 1 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- June 1945
-
- Article
-
- You have access
- Export citation
Covariant line complexes of a pair of quadric surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 2 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 127-135
- Print publication:
- June 1945
-
- Article
- Export citation
Totally heterogeneous continua
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 2 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. 96-103
- Print publication:
- June 1945
-
- Article
- Export citation
PSP volume 41 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 41 / Issue 2 / June 1945
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- June 1945
-
- Article
-
- You have access
- Export citation
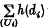 for any such sequence {
for any such sequence {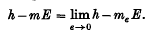
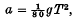 where
where 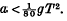 .
.