1. The present paper deals with an enclosed (linear) harmonic oscillator. The usual boundary condition that the wave function vanishes at infinity is here replaced by the condition that the wave function vanishes at the walls of the enclosure. The problem has been treated before (1, 2, 4). However, the present discussion goes much further than that given in the papers cited*.

During the course of some investigations on the distribution of stress in an elastic solid it was noticed by the senior author that a systematic application of the method of integral transforms to the problem of the indentation of the plane surface of a semi-infinite elastic solid by a rigid punch reduced the problem essentially to one of solving a pair of integral equations belonging to a class which has been studied by Titchmarsh and by Busbridge (4,5). This procedure allows one to obtain the solution for an arbitrary shape of punch by a general method which leads automatically to the solution and avoids the troublesome procedure, adopted by Love (2) in the case of a conical punch, of being obliged to guess appropriate combinations of solutions which will satisfy the prescribed boundary conditions in any special case. Moreover, it can easily be seen that an attempt to apply Love's method to more complicated shapes of punch will lead to considerable analytical difficulties.

We are concerned in this paper with linear integro-differential equations of the form*

and

where kr(y) are given functions with bounded variation in any finite interval, g(x) is known, and f(x) is to be determined.

1. I proved in 1908(1) that if A = Σam and B = Σbn are convergent, and

for large m and n, then

is convergent (necessarily to AB); and this theorem has been extended in a number of directions both by other writers and by myself. Thus we may replace (1), when am and bn are real, by

we may use conditions unsymmetrical in am and bn; we may put the same problem for the product of any number of series; and we may consider modes of ‘Dirichlet multiplication’ based on sequences λm and μn, reducing to Cauchy's when λm = m and μn = n. The appropriate references will be found in(2).

There are several mistakes and misprints in the above paper.

(1) In introducing Voigt's notation for the strain components the well-known factor 2 in the normal components has been omitted, and (3·11) should read

The following formulae in which this notation is used are correct as they stand.

1. We first compare the λ-ic characters of two polynomials with respect to each other and the prime p, the polynomials being irreducible with respect to p. This is done by relating each to the resultant of the polynomials. We then show in § 6 that the ordinary quadratic character of one prime with respect to another is also the resultant of two polynomials.

It has been found possible to generalize Ising's (4) treatment of the linear chain with nearest-neighbour interaction, and his main result, that such interaction cannot lead to cooperative effects, has been shown to hold for very many, if not all, types of lattice in three dimensions. Reasons are given for presuming a similar result for the second nearest-neighbour model. It is found, however, that even a small interaction of the long-range type can lead to cooperative effects at high temperatures, provided that the nearest-neighbour interaction is sufficiently strong. It is therefore claimed that explicit account must be taken of both types of interaction in any acceptable theory, and a possible method of estimating their relative importance is indicated.

1. In this paper an analysis is given of the distribution of stress in a semi-infinite elastic medium due to the action of an external force applied to the interior of the medium. It will be assumed throughout that the force acts in a direction perpendicular to that of the boundary of the solid; the analysis is similar when the line of action of the force is parallel to the boundary and is therefore not given here. The equations of plane strain parallel to the x-y plane are employed; physically this is equivalent to assuming that there is no component of the displacement vector in a direction normal to the x-y plane or, what is the same thing, that the external force is applied along are infinite line parallel to the axis of z.

1. Let a, b be positive constants; and let y1, y2, …, yn be real exponents, not all equal, having arithmetic mean y defined by

(here, and in what follows, the summation ∑ extends over the values i = 1, 2, …, n). Then it is clear that

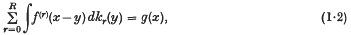
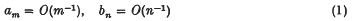
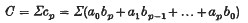
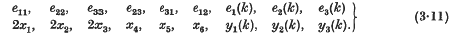
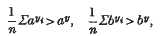
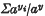since the right-hand sides are the geometric means of the positive numbers whose arithmetic means stand on the left-hand sides. I know of no results, however, which relate the ratios and 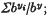and I have had occasion recently to require such results. This note gives an inequality between these ratios, subject to certain restrictions on a and b.

1. A method has lately been developed by N. Muschelišvili (1) for the solution of problems of the slow two-dimensional motion of viscous liquid and of the corresponding problems of plane stress and plane strain, in cases in which the area in the x, y-plane that is concerned can be represented conformally on the interior of the circle |ζ| = 1 in the ζ-plane by a relation of the form z = x + iy = r(ζ), where r(ζ) is a rational function of ζ. In most problems in which the method has been used the function r(ζ) has been a simple one, but it is of importance to consider a rational function of as general a form as possible since, given any relation z = f(ζ), it will usually be possible to find a rational function that approximates to f(ζ) throughout the circle |ζ| = 1 and for a close approximation a complicated function r(ζ) will in general be required.

3. The essential requirement that the nova must satisfy in the above theory is that the total mass in the form of diffuse gaseous material must be of the order of 1/10 the solar mass, which requirement seems to be consistent with the observations of novae. Thus, although the theory applies explicitly to novae that break into two pieces of stellar mass having a gaseous filament drawn out between them (the pieces may have a mass ratio as great as 5/1), it seems clear that the discussion could be adjusted to include the case of novae following other models.

The process described above can be applied to the formation of non-solar planets. The mass of available planetary material depends upon such factors as the mass of the nova and its separation from the companion before outburst. It is to be expected that variations in these factors can lead to planetary masses that vary over a fairly wide range. It follows that since an appreciable fraction of the stars of mass comparable or greater than the solar mass are known to be members of binary systems, the number of planetary systems must be at least of the same order as the number of novae that have occurred in this class of star.

1. Problems in elasticity which are concerned with isotropic rectangular plates have attracted the attention of many writers both from the theoretical and practical points of view. When the boundary conditions are of the simply supported type the solution of the problems is usually simple, although when double Fourier series are used the validity of such solutions is not very clearly shown in most cases. Satisfactory exact solutions for many classical problems in which the edges of the rectangular plate are clamped have only been obtained in recent years, but approximate strain energy methods often gave results which were useful for practical purposes.

Stokes and Wilson(1,2) have shown that the integral breadths of the Debye-Scherrer lines produced by small or imperfect crystals of the cubic system are given by

or, what is the same thing, that the apparent particle sizes are given by

In these equations λ is the X-ray wave-length, θ is the Bragg angle, Vt is the volume common to the crystal and its ‘ghost’ shifted a distance t in the hkl direction(1), and Jt is the mean value of the product FF of the structure amplitudes of two cells separated by a distance t in the hkl direction (2). The purpose of this note is to outline an argument which establishes the same result for crystals of any symmetry.

In an improved method of strip-theory calculation of the performance of an airscrew a factor K occurs in the formula

which, for an airscrew with N blades, connects the total interference velocity w1 and the circulation Γ at radius r. In this formula ø is the inclination to the plane of rotation of the airscrew of the velocity of the air relative to the airscrew blade; for infinite pitch ø=½π For large but finite pitch the calculation of K is difficult; in computing tables of K it is therefore useful to have the values for infinite pitch, which can be calculated by a much simpler theory than that needed for the general case†.