The production of a ‘wake’ behind solid bodies has been treated by different authors. S. Goldstein (1) and S. H. Hollingdale (2) have discussed the laminar wake behind a flat plate, while the wake of a two-dimensional grid has been treated for the turbulent case alone using L. Prandtl's ‘Mischungsweg’ theory by E. Anderlik and Gran Olsson (3), (4).

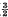In three papers (1, 2, 3) Bhabha has set up a new theory for relativistic particles of any spin, and has suggested that a particular wave equation of half-odd spin, classified as (, ½), may be applicable to the proton. It is therefore of interest to study this equation and to calculate results which could perhaps be compared with experiment; since in the non-relativistic limit the particle obeys Dirac's equation, it is sufficient to consider the behaviour at energies large compared to the rest mass. Here the important problem is the calculation of scattering cross-sections for cosmic-ray processes.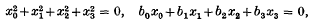

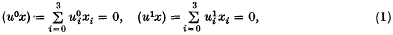
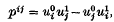
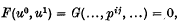
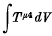After solving the equations of motion of Dirac's self-accelerating electron, a physical picture of it is formed by plotting graphically the surfaces of constant scalar potential when the electron has built up a velocity close to the velocity of light.

It was in a paper bearing this title that Cayley(1) first considered the problem of representing a curve in projective space of three dimensions by means of the complex of lines which meet the curve. He took the conic given by the equations

and found that the line

with dual Grassmann coordinates (…,pij,…), where

intersects the conic if, and only if,

where F(u0, u1) is homogeneous and of degree 2 in both sets of indeterminates u0 and u1 and G(…,pij,…) is a form of degree 2 in the pij. Both F(u0, u1) and G(…,pij,…) are easily determined in this case.

We begin with some definitions.

A cubical graph is a simplicial 1-complex in which each 0-simplex is incident with just three 1-simplexes.

1. The theoretical study of the transport phenomena in metals requires the solution of a certain integral equation, which is formed by equating the rate of change of the distribution function of the conduction electrons due to the applied fields and temperature gradients to the rate of change due to the mechanism responsible for the scattering. This integral equation has so far been solved only in the simplest case where the electrons are assumed to be quasi-free, the energy being proportional to the square of the wave vector, and this assumption will be made throughout the present paper. The scattering of the electrons is due to two causes: the thermal vibration of the crystal lattice and the presence of impurities or strains. The scattering due to the impurities can always be described in terms of a free path l (or more conveniently a time of relaxation τ, were l = τν, ν being the average velocity of the conduction electrons), whereas for the scattering due to the thermal vibration this is possible only at high temperatures such that (Θ/T)2 can be neglected, where Θ is the Debye temperature (1). At very low temperatures the scattering due to the thermal vibration can be neglected compared with that due to the impurities. When a time of relaxation exists, the integral equation for the distribution function reduces to an ordinary equation, and its solution is then a comparatively simple matter. In the general case the problem is much more difficult, and no rigorous and generally valid solution has so far been obtained.

A short discussion of steady rectilinear plastic flow of Bingham material between rigid cylinders of general shape in relative motion parallel to their generators was given in a paper of the same main title(1). It was shown that, for sufficiently great relative velocity V of the boundaries, plastic flow in the whole region would be expected, as for a Newtonian liquid. But for slower relative motion, part of the material might remain elastically deformed (i.e. stressed below the yield point) with a limited region of plastic flow surrounding the inner boundary. In the paper referred to, the problem was illustrated by the case of eccentric circular cylindrical boundaries. The choice of circular boundaries introduced a great simplification when the region of plastic flow did not extend to the outer boundary, namely axial symmetry in the flow pattern in the plastic region. It is the main purpose of the present paper to illustrate how the methods already given for determining velocity distributions may be modified to suit more general problems, by consideration of confocal elliptic cylinders as boundaries.

In relativistic field theories derived by a variation principle from a Lagrangian, the problem arises of finding a symmetric tensor of rank 2 which has vanishing divergence in virtue of the field equations and is such that taken over a space-like section is equal to the corresponding integral of the so-called canonical energy-momentum tensor. It is well known that the latter condition is satisfied if the difference between the two tensors is the divergence of an antisymmetric tensor of rank 3.

Let r, s be two fixed integers greater than 1. A positive integer will be called r-free if it is not divisible by the rth power of any prime.

In a series of papers ((l)–(5)) Evelyn and Linfoot considered the problem of determining an asymptotic formula for the number Qr, s(n) of representations of a large positive integer n as the sum of s r-free integers; for s ≥ 4 their results were subsequently sharpened by Barham and Estermann(6).

An account is given of the transformation of coordinates and of absolute axial frames in Euclidean space and Galilean space-time. The connexion with Eddington's group of E-numbers is shown. The geometrical properties of Dirac's wave equation and of analogous equations in three dimensions are discussed in terms of absolute axial frames.

1. In the first paper of this series I have explained a method by which the complete irreducible system of combinants of a pencil of quadric surfaces may be obtained, and have determined explicitly the combinantal invariants and covariants. The present paper deals with combinantal contravariants. The notation used is that of I, a knowledge of which will be assumed.