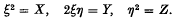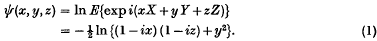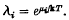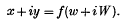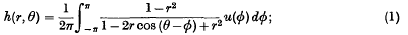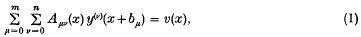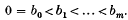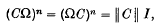Refine search
Actions for selected content:
26207 results in Theoretical Physics and Mathematical Physics
Two New Almanacs - (i) Altitude and Azimuth Almanac for August–December 1947. Hydrographic Department, Japan; May 1947; vi + 93 pages; paper covers, 7·2 × 10·2 inches ; no price stated.
-
- Journal:
- The Journal of Navigation / Volume 1 / Issue 2 / May 1948
- Published online by Cambridge University Press:
- 18 January 2010, pp. 185-187
- Print publication:
- May 1948
-
- Article
- Export citation
Time Determination and Time Keeping
-
- Journal:
- The Journal of Navigation / Volume 1 / Issue 2 / May 1948
- Published online by Cambridge University Press:
- 18 January 2010, pp. 109-117
- Print publication:
- May 1948
-
- Article
- Export citation
Rectilinear plastic flow of a Bingham solid: IV. Non-steady motion
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 214-228
- Print publication:
- April 1948
-
- Article
- Export citation
Note on Peng's treatment of the divergency difficulties in quantized field theories
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 301-303
- Print publication:
- April 1948
-
- Article
- Export citation
The arithmetical character of the Wishart distribution
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 295-297
- Print publication:
- April 1948
-
- Article
- Export citation
The condition for the detachment of the shock wave from a wedge in a supersonic stream
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 298-300
- Print publication:
- April 1948
-
- Article
- Export citation
PSP volume 44 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- April 1948
-
- Article
-
- You have access
- Export citation
On one-dimensional regular assemblies
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 263-271
- Print publication:
- April 1948
-
- Article
- Export citation
Rectilinear plastic flow of a Bingham solid: III. A more general discussion of steady flow
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 200-213
- Print publication:
- April 1948
-
- Article
- Export citation
Expansions in terms of sets of functions with complex eigenvalues
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 242-250
- Print publication:
- April 1948
-
- Article
- Export citation
Combinants of a pencil of quadric surfaces (IV)*
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 196-199
- Print publication:
- April 1948
-
- Article
- Export citation
The theory of neutral particles
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 229-241
- Print publication:
- April 1948
-
- Article
- Export citation
On perturbation problems associated with finite boundaries
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 251-262
- Print publication:
- April 1948
-
- Article
- Export citation
Inequalities for the derivatives of a bounded harmonic function
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 155-158
- Print publication:
- April 1948
-
- Article
- Export citation
Linear difference-differential equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 179-185
- Print publication:
- April 1948
-
- Article
- Export citation
Thermal conductivity of copper and german silver at liquid helium temperatures
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 280-288
- Print publication:
- April 1948
-
- Article
- Export citation
Some inequalities in the theory of functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 159-178
- Print publication:
- April 1948
-
- Article
- Export citation
On the matrix equation (AX)n = ∥A∥I
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 292-294
- Print publication:
- April 1948
-
- Article
- Export citation
The lattice properties of asymmetric hyperbolic regions: II. On a theorem of davenport
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 145-154
- Print publication:
- April 1948
-
- Article
- Export citation
PSP volume 44 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 2 / April 1948
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- April 1948
-
- Article
-
- You have access
- Export citation