Refine search
Actions for selected content:
26207 results in Theoretical Physics and Mathematical Physics
A New System of Compass Correction
-
- Journal:
- The Journal of Navigation / Volume 1 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 18 January 2010, pp. 197-218
- Print publication:
- July 1948
-
- Article
- Export citation
Radar and the Weather
-
- Journal:
- The Journal of Navigation / Volume 1 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 18 January 2010, pp. 219-240
- Print publication:
- July 1948
-
- Article
- Export citation
The breakdown of the hodograph transformation for irrotational compressible fluid flow in two dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 360-379
- Print publication:
- July 1948
-
- Article
- Export citation
The statistical distribution of the length of a rubber molecule
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 342-344
- Print publication:
- July 1948
-
- Article
- Export citation
The Instrumental Accuracy Required for Barometric Drift Estimation
-
- Journal:
- The Journal of Navigation / Volume 1 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 18 January 2010, pp. 262-265
- Print publication:
- July 1948
-
- Article
- Export citation
Some probability distributions connected with recording apparatus
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 335-341
- Print publication:
- July 1948
-
- Article
- Export citation
The Johnston Air Navigation Trophy
-
- Journal:
- The Journal of Navigation / Volume 1 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 18 January 2010, p. 272
- Print publication:
- July 1948
-
- Article
- Export citation
On the dynamical theory of the rotation of the earth: I. The secular retardation of the core
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 345-359
- Print publication:
- July 1948
-
- Article
- Export citation
Applied D.R. Navigation and Flight Planning. J. H. Clough-Smith, SirIsaac Pitman, 1947; 241, vi; cloth; 8·8 × 5·6 inches; price 22s. 6d.
-
- Journal:
- The Journal of Navigation / Volume 1 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 18 January 2010, p. 280
- Print publication:
- July 1948
-
- Article
- Export citation
NAV volume 1 issue 3 Back matter
-
- Journal:
- The Journal of Navigation / Volume 1 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 18 January 2010, p. b1
- Print publication:
- July 1948
-
- Article
-
- You have access
- Export citation
The half-life of thorium C′
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 440-446
- Print publication:
- July 1948
-
- Article
- Export citation
The Sailor in the Middle Ages
-
- Journal:
- The Journal of Navigation / Volume 1 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 18 January 2010, pp. 191-196
- Print publication:
- July 1948
-
- Article
- Export citation
Aids to Land Navigation
-
- Journal:
- The Journal of Navigation / Volume 1 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 18 January 2010, p. 282
- Print publication:
- July 1948
-
- Article
-
- You have access
- Export citation
A Revised Formula for Calculating the Dip of the Sea Horizon
-
- Journal:
- The Journal of Navigation / Volume 1 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 18 January 2010, p. 272
- Print publication:
- July 1948
-
- Article
- Export citation
Liverpool Harbour Supervision Radar
-
- Journal:
- The Journal of Navigation / Volume 1 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 18 January 2010, p. 271
- Print publication:
- July 1948
-
- Article
- Export citation
Right-Angled Side Lights
-
- Journal:
- The Journal of Navigation / Volume 1 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 18 January 2010, pp. 270-271
- Print publication:
- July 1948
-
- Article
- Export citation
Coloured Charts
-
- Journal:
- The Journal of Navigation / Volume 1 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 18 January 2010, p. 272
- Print publication:
- July 1948
-
- Article
- Export citation
Certain integral representations for Whittaker functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 453-455
- Print publication:
- July 1948
-
- Article
- Export citation
Quantum mechanics of the anharmonic oscillator
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 44 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 24 October 2008, pp. 413-422
- Print publication:
- July 1948
-
- Article
- Export citation
The Earthed Antenna
-
- Journal:
- The Journal of Navigation / Volume 1 / Issue 3 / July 1948
- Published online by Cambridge University Press:
- 18 January 2010, pp. 281-282
- Print publication:
- July 1948
-
- Article
-
- You have access
- Export citation
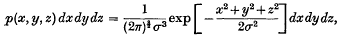
 and
and  then
then