Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
Note on the transparency of a potential barrier
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 4 / November 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 401-405
- Print publication:
- November 1942
-
- Article
- Export citation
On certain expansions of the solutions of the general Lamé equation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 4 / November 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 364-367
- Print publication:
- November 1942
-
- Article
- Export citation
On the reflexion of a spherical sound pulse by a parabolic mirror
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 4 / November 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 383-393
- Print publication:
- November 1942
-
- Article
- Export citation
The postulation of a multiple curve
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 4 / November 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 368-377
- Print publication:
- November 1942
-
- Article
- Export citation
The Cambridge Philosophical Society Statement of Accounts for the Period 1 August 1940 to 31 July 1941
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 4 / November 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 408-409
- Print publication:
- November 1942
-
- Article
- Export citation
On the solutions of the wave equation with discontinuous derivatives
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 4 / November 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 378-382
- Print publication:
- November 1942
-
- Article
- Export citation
On the theory of successive radioactive transformations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 3 / July 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 280-289
- Print publication:
- July 1942
-
- Article
- Export citation
Note on an anomaly in the spectrum of O++
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 3 / July 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 290-295
- Print publication:
- July 1942
-
- Article
- Export citation
The influence of radiation damping on the scattering of mesons: II. Multiple processes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 3 / July 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 296-312
- Print publication:
- July 1942
-
- Article
- Export citation
A method of calculating the integral breadths of Debye-Scherrer lines
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 3 / July 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 313-322
- Print publication:
- July 1942
-
- Article
- Export citation
A generalization of additive ideal theory
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 3 / July 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 241-279
- Print publication:
- July 1942
-
- Article
- Export citation
An infinite integral
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 3 / July 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 323-324
- Print publication:
- July 1942
-
- Article
- Export citation
PSP volume 38 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 3 / July 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- July 1942
-
- Article
-
- You have access
- Export citation
PSP volume 38 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 3 / July 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- July 1942
-
- Article
-
- You have access
- Export citation
PSP volume 38 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- April 1942
-
- Article
-
- You have access
- Export citation
A remark on a property of a special pencil of quadrics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 234-235
- Print publication:
- April 1942
-
- Article
- Export citation
Note on the degeneration of algebraic varieties
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 231-233
- Print publication:
- April 1942
-
- Article
- Export citation
The thermodynamic derivation of Fowler's adsorption isotherm
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 236-239
- Print publication:
- April 1942
-
- Article
- Export citation
On Lorentz invariance in the quantum theory
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 193-200
- Print publication:
- April 1942
-
- Article
- Export citation
PSP volume 38 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- April 1942
-
- Article
-
- You have access
- Export citation
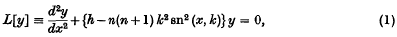

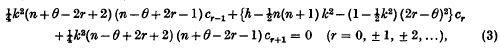
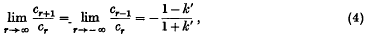
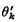 of ϲ′.
of ϲ′.