Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
On the generalized helices of Hayden and Sypták in an N-space
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 229-243
- Print publication:
- July 1941
-
- Article
- Export citation
A new type of disintegration produced by deuterons
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 317-323
- Print publication:
- July 1941
-
- Article
- Export citation
PSP volume 37 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- July 1941
-
- Article
-
- You have access
- Export citation
PSP volume 37 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- July 1941
-
- Article
-
- You have access
- Export citation
On the theory of the liquid state: III. The hole theory of the viscous flow of liquids
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 281-290
- Print publication:
- July 1941
-
- Article
- Export citation
On the theory of the liquid state: I. The statistical treatment of the thermodynamics of liquids by the theory of holes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 252-275
- Print publication:
- July 1941
-
- Article
- Export citation
The influence of radiation damping on the scattering of light and mesons by free particles. I
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 291-300
- Print publication:
- July 1941
-
- Article
- Export citation
On the theory of the liquid state: II. Application of the hole theory to superheated liquids and supersaturated solutions of gases in liquids
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 276-280
- Print publication:
- July 1941
-
- Article
- Export citation
The fractional dimensional theory of continued fractions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 199-228
- Print publication:
- July 1941
-
- Article
- Export citation
The action in a uniform field
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 2 / April 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 168-176
- Print publication:
- April 1941
-
- Article
- Export citation
The motion of a solid through an infinite liquid under no forces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 2 / April 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 150-167
- Print publication:
- April 1941
-
- Article
- Export citation
The reflexion of sound pulses by convex parabolic reflectors
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 2 / April 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 134-149
- Print publication:
- April 1941
-
- Article
- Export citation
Deuteron bombardment of gold
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 2 / April 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 186-193
- Print publication:
- April 1941
-
- Article
- Export citation
On sets of fractional dimensions (II)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 2 / April 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 127-133
- Print publication:
- April 1941
-
- Article
- Export citation
PSP volume 37 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 2 / April 1941
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- April 1941
-
- Article
-
- You have access
- Export citation
On colouring the nodes of a network
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 2 / April 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 194-197
- Print publication:
- April 1941
-
- Article
- Export citation
Sur les familles indenombrables de suites de nombres naturels et les problemes concernant la propriete C
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 2 / April 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 109-126
- Print publication:
- April 1941
-
- Article
- Export citation
On the stability of crystal lattices: VI. The properties of matter under high pressure and the lattice theory of crystals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 2 / April 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 177-185
- Print publication:
- April 1941
-
- Article
- Export citation
PSP volume 37 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 2 / April 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- April 1941
-
- Article
-
- You have access
- Export citation
On an Infinite Integral Connected with the Theory of Bessel Functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 1 / January 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 102-104
- Print publication:
- January 1941
-
- Article
- Export citation

 taking place, in all probability, through the formation of a ‘compound nucleus’ of the Bohr type.
taking place, in all probability, through the formation of a ‘compound nucleus’ of the Bohr type.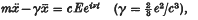
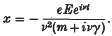
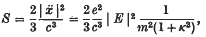
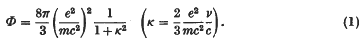
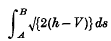
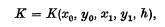
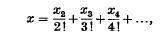
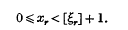
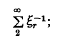
 et
et  respectivement l'ensemble des nombres rationnels et l'ensemble des nombres irrationnels de cet intervalle.
respectivement l'ensemble des nombres rationnels et l'ensemble des nombres irrationnels de cet intervalle.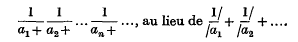
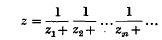
 correspond à une famille Φ de suites de nombres naturels si l'on a
correspond à une famille Φ de suites de nombres naturels si l'on a 