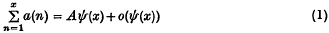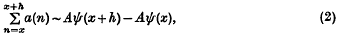Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
On the fractional parts of the powers of a number (II)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 349-357
- Print publication:
- October 1941
-
- Article
- Export citation
Deuteron bombardment of the heavy elements: II. Platinum
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 422-432
- Print publication:
- October 1941
-
- Article
- Export citation
The sputtering of platinum in hydrogen and deuterium
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 438-439
- Print publication:
- October 1941
-
- Article
- Export citation
A method of making stream-lines momentarily visible
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 436-437
- Print publication:
- October 1941
-
- Article
- Export citation
Notes on special systems of orthogonal functions (IV): the orthogonal functions of whittaker's cardinal series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 331-348
- Print publication:
- October 1941
-
- Article
- Export citation
Surface motion of sputtered particles
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 440-442
- Print publication:
- October 1941
-
- Article
- Export citation
On a conjecture of Mordell concerning binary cubic forms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 325-330
- Print publication:
- October 1941
-
- Article
- Export citation
PSP volume 37 issue 4 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b10
- Print publication:
- October 1941
-
- Article
-
- You have access
- Export citation
Proceedings at the Meetings held during the Session 1940–1941
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 443-445
- Print publication:
- October 1941
-
- Article
- Export citation
The Cambridge Philosophical Society Statement of Accounts for the Period 1 August 1939 to 31 July 1940
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 446-447
- Print publication:
- October 1941
-
- Article
- Export citation
PSP volume 37 issue 4 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- October 1941
-
- Article
-
- You have access
- Export citation
Momentum distribution in molecular systems: Part IV. The hydrogen molecular ion
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 397-405
- Print publication:
- October 1941
-
- Article
- Export citation
Notes on the two-centre problem in wave mechanics: II. Some new solutions of the wave equation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 384-396
- Print publication:
- October 1941
-
- Article
- Export citation
Momentum distribution in molecular systems: Part V. Momentum distribution and the shape of the Compton line for CH4, C2H6, C2H4 and C2H2
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 406-421
- Print publication:
- October 1941
-
- Article
- Export citation
Note on semi-groups
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 434-435
- Print publication:
- October 1941
-
- Article
- Export citation
A proof of the theorem of the double-six
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 433-434
- Print publication:
- October 1941
-
- Article
- Export citation
On the subadditivity of the transfinite diameter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 373-383
- Print publication:
- October 1941
-
- Article
- Export citation
On average values of arithmetic functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 358-372
- Print publication:
- October 1941
-
- Article
- Export citation
The quantum theory of radiation damping‡
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 301-316
- Print publication:
- July 1941
-
- Article
- Export citation
The probability distribution of the extent of a random chain
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 244-251
- Print publication:
- July 1941
-
- Article
- Export citation
 reaction.
reaction.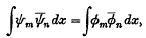
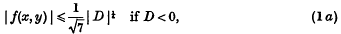
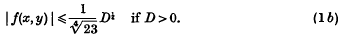
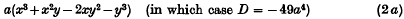
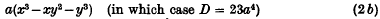
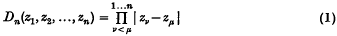
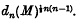 Then it can be proved that
Then it can be proved that