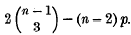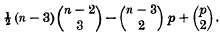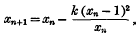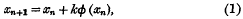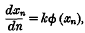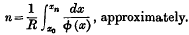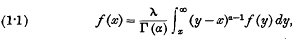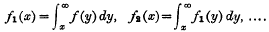Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
PSP volume 28 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 3 / July 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- July 1932
-
- Article
- Export citation
Inverse probability and the use of Likelihood
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 3 / July 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 257-261
- Print publication:
- July 1932
-
- Article
- Export citation
The motion of electrons in the field of excited, helium
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 3 / July 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 341-348
- Print publication:
- July 1932
-
- Article
- Export citation
The number of apparent double points of certain loci
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 3 / July 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 285-299
- Print publication:
- July 1932
-
- Article
- Export citation
The interaction of lattice vibrations and free electrons in metals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 3 / July 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 367-385
- Print publication:
- July 1932
-
- Article
- Export citation
A measurement of Boltzmann's constant by means of the fluctuations of electron pressure in a conductor
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 3 / July 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 386-402
- Print publication:
- July 1932
-
- Article
- Export citation
On the Riemann zeta-function
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 3 / July 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 273-274
- Print publication:
- July 1932
-
- Article
- Export citation
On Boole's operational solution of linear finite difference equations with rational coefficients
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 3 / July 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 311-318
- Print publication:
- July 1932
-
- Article
- Export citation
A note on integral functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 3 / July 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 262-265
- Print publication:
- July 1932
-
- Article
- Export citation
Some surfaces containing triple curves
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 3 / July 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 300-310
- Print publication:
- July 1932
-
- Article
- Export citation
A note on analytic functions in the unit circle
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 3 / July 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 266-272
- Print publication:
- July 1932
-
- Article
- Export citation
Absorption measurements and the continuous spectrum of β-rays
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 3 / July 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 319-327
- Print publication:
- July 1932
-
- Article
- Export citation
A mathematical theory of natural and artificial selection. Part IX. Rapid selection
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 2 / April 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 244-248
- Print publication:
- April 1932
-
- Article
- Export citation
Note on the trisecants and quadrisecants of a space curve
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 2 / April 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 206-208
- Print publication:
- April 1932
-
- Article
- Export citation
On the canonical curve of genus five
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 2 / April 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 174-189
- Print publication:
- April 1932
-
- Article
- Export citation
On the non-linear difference equation Δxn = kΦ (xn)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 2 / April 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 234-243
- Print publication:
- April 1932
-
- Article
- Export citation
An integral equation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 2 / April 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 165-173
- Print publication:
- April 1932
-
- Article
- Export citation
PSP volume 28 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 2 / April 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- April 1932
-
- Article
- Export citation
PSP volume 28 issue 2 Cover, Front matter and Corrigenda
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 2 / April 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f3
- Print publication:
- April 1932
-
- Article
- Export citation
The energy exchanges between molecules
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 28 / Issue 2 / April 1932
- Published online by Cambridge University Press:
- 24 October 2008, pp. 249-255
- Print publication:
- April 1932
-
- Article
- Export citation
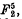 the only non-ruled quintic surface in [5], has one apparent double point; Babbage shows that this surface is a member of a series of loci
the only non-ruled quintic surface in [5], has one apparent double point; Babbage shows that this surface is a member of a series of loci 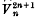 in [2
in [2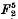 by means of cubic curves through four fixed points.
by means of cubic curves through four fixed points.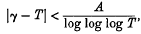



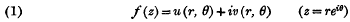
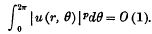
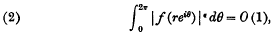
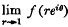
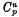 of order
of order