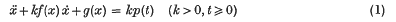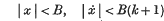Refine search
Actions for selected content:
26208 results in Theoretical Physics and Mathematical Physics
The Double Altitude Problem
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, p. 108
- Print publication:
- January 1951
-
- Article
-
- You have access
- Export citation
Ciro Caric's Tables
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 105-106
- Print publication:
- January 1951
-
- Article
-
- You have access
- Export citation
Statistical mechanics and partitions into non-integral powers of integers
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 207-216
- Print publication:
- January 1951
-
- Article
- Export citation
The theoretical behaviour of a magnetic monopole in a wilson cloud chamber
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 196-206
- Print publication:
- January 1951
-
- Article
- Export citation
A note on rayleigh's problem for a plate of finite width
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 248-250
- Print publication:
- January 1951
-
- Article
- Export citation
A boundedness theorem for non-linear differential equations of the second order
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 49-54
- Print publication:
- January 1951
-
- Article
- Export citation
An Investigation into Air Traffic Control by a Simulation Method
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 34-65
- Print publication:
- January 1951
-
- Article
- Export citation
An extension of the law of the iterated logarithm
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 55-64
- Print publication:
- January 1951
-
- Article
- Export citation
NAV volume 3 issue 4 Cover and Front matter
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. f1-f16
- Print publication:
- October 1950
-
- Article
-
- You have access
- Export citation
Use of Direction Finding at Sea
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 332-335
- Print publication:
- October 1950
-
- Article
- Export citation
II—Some Problems of Interplanetary Navigation
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 365-377
- Print publication:
- October 1950
-
- Article
- Export citation
Stochastic processes relating to particles distributed in a continuous infinity of states
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 595-602
- Print publication:
- October 1950
-
- Article
- Export citation
The characterization of quantum-mechanical operators
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 614-619
- Print publication:
- October 1950
-
- Article
- Export citation
A note on magnetic fields in conducting materials
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 651-654
- Print publication:
- October 1950
-
- Article
- Export citation
Unsteady laminar flow of gas near an infinite flat plate
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 603-613
- Print publication:
- October 1950
-
- Article
- Export citation
An Altitude Correction Computer
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 385-388
- Print publication:
- October 1950
-
- Article
- Export citation
A further note on trigonometrical inequalities
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 535-537
- Print publication:
- October 1950
-
- Article
- Export citation
Sets of uniqueness for trigonometric series and integrals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 538-548
- Print publication:
- October 1950
-
- Article
- Export citation
The Development of the Aircraft Automatic Radio Compass
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 393-403
- Print publication:
- October 1950
-
- Article
- Export citation
Proceedings at the Meetings Held During the Session 1949–1950: Annual General Meeting
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 655-658
- Print publication:
- October 1950
-
- Article
- Export citation