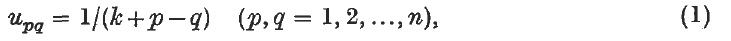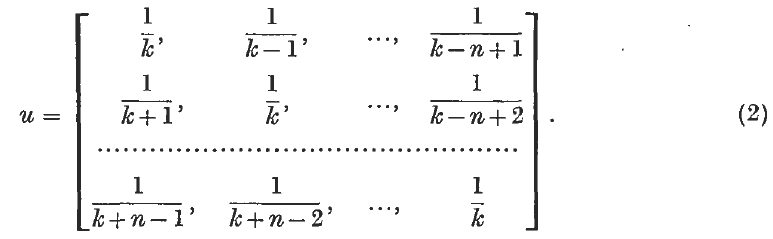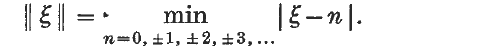Refine search
Actions for selected content:
26208 results in Theoretical Physics and Mathematical Physics
Navigation and the Aircraft Industry
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 1-11
- Print publication:
- January 1951
-
- Article
- Export citation
Proposals for a New Air Navigation Chart
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 66-80
- Print publication:
- January 1951
-
- Article
- Export citation
Triple velocity correlations in isotropic turbulence
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 146-157
- Print publication:
- January 1951
-
- Article
- Export citation
On the reciprocal of a segment of a generalized hilbert matrix
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 11-17
- Print publication:
- January 1951
-
- Article
- Export citation
Some metrical theorems in diophantine approximation: v. on a conjecture of mahler
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 18-21
- Print publication:
- January 1951
-
- Article
- Export citation
Slow motion of viscous liquid in a semi-infinite channel
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 127-141
- Print publication:
- January 1951
-
- Article
- Export citation
The Work of Trinity House
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 86-92
- Print publication:
- January 1951
-
- Article
- Export citation
A reduction for the matrix equation AB = εBA
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 7-10
- Print publication:
- January 1951
-
- Article
- Export citation
PSP volume 47 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- January 1951
-
- Article
-
- You have access
- Export citation
On the line-comitants of a space cubic
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 46-48
- Print publication:
- January 1951
-
- Article
- Export citation
An extremal property of the hypersphere
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 245-247
- Print publication:
- January 1951
-
- Article
- Export citation
Markoff chains with an enumerable number of states and a class of cascade processes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 77-85
- Print publication:
- January 1951
-
- Article
- Export citation
The Selection of Stars for Astronomical Navigation
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 31-33
- Print publication:
- January 1951
-
- Article
- Export citation
NAV volume 4 issue 1 Front matter
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. f1-f4
- Print publication:
- January 1951
-
- Article
-
- You have access
- Export citation
The relativistic mass of a rotating cylinder
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 190-195
- Print publication:
- January 1951
-
- Article
- Export citation
An Almanac for Surveyors - The Star Almanac for Land Surveyors for the year 1951, prepared by H.M. Nautical Almanac Office. H.M. Stationery Office, 1950. 3s.
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, p. 104
- Print publication:
- January 1951
-
- Article
- Export citation
PSP volume 47 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- January 1951
-
- Article
-
- You have access
- Export citation
The frequency goodness of fit test for probability chains
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 86-95
- Print publication:
- January 1951
-
- Article
- Export citation
Meteorology and Airfield Design - Meteorology of Airfields. C. S. Durst, B.A. (Meteorological Office publication 507). H.M. Stationery Office, 1949, 87 pp., paper 9·6 × 6 in., 2s.
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 100-101
- Print publication:
- January 1951
-
- Article
- Export citation
A process for the step-by-step integration of differential equations in an automatic digital computing machine
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 96-108
- Print publication:
- January 1951
-
- Article
- Export citation