We consider n − 1 points xj (j = 1, …, n − 1) selected independently at random from the interval (0, 1), the distribution of any xj being the rectangular distribution

The points xj divide the interval (0,1) into n intervals. Let λ be the sum of the lengths of the k largest of these n intervals. It is the purpose of this paper to give the exact sampling distribution of λ for any given n and k (see equation (5)). Fisher (1) in 1929 solved the problem for k = 1. We first investigate the distribution of μ = 1 − λ.

The object of the present paper is to discuss the Fourier expansion of the Riesz potential. For this purpose a new definition of the electromagnetic potentials, depending upon an arbitrary parameter α is given. It is shown that this definition is a generalization of the Wentzel potentials in the α-plane, whereas that given by Fremberg (3) is a generalization of the Maxwell potentials. The analysis is applied to the problem of eliminating, in a straightforward way, the longitudinal part of the potential describing the electromagnetic field. The problem of the quantization of the field, based on its Fourier expansion, will be considered in another paper. The recent work of Tomonaga, Schwinger and Dyson, and the regularization process of Pauli has lifted the theory of quantum electrodynamics to a much higher level of rigour and fruitful applicability. All the same, a further study of Riesz potential seems to us of some interest in this field.

The British standard blind flying panel and its component instruments have for many years fulfilled a very useful purpose, but there are now a number of special operational requirements which this panel no longer meets. For instance, the probable general use of tail warning devices will make it necessary for the night fighter pilot to follow the violent evasive action of his quarry, and because of the higher speeds involved it is desirable that the pilot should be able to interpret his radar scopes himself rather than depend upon his navigator for directions.

The equation of steady rectilinear motion of a material of variable viscosity is transformed, when the pressure gradient vanishes, into a second-order differential equation which is linear in the dependent variable. A general solution of the linearized equation can be obtained in the case of a wide class of plastic solids and viscous liquids. By making use of the idealized materials which lend themselves to this method of solution, a theoretical comparison can be made of the behaviour of plastic solids of different types under the same conditions. As an illustration, a plastic solid which yields very sharply when the yield point is first exceeded is compared with one which yields only gradually at the same yield value; the flow caused by the longitudinal motion of an (approximately) elliptic cylinder in an infinite mass of material is investigated in each case.

Suppose that dυ and dυ′ are two volume elements situated at points P and P′ respectively in a three-dimensional right circular cylinder, that y is the distance PP′, that z(y) is a given function of y, and that we wish to evaluate the sixfold integral

taken over all pairs of points P, P′ within the cylinder. We observe that z(y) is a function of y only; so that the sixfold integral can be expressed as a single integral

that is to say a weighted mean of z(y) over the relevant values of y, where the weight function is evidently given by

Let X denote the general point with coordinates (x1, x2, x3) in 3-dimensional space; and let P(X) be the function defined by

This paper considers the correlation P(r) between the fluctuating pressures at two different points distance r apart in a field of homogeneous isotropic turbulence. P(r) can be expressed in terms of the fourth moment of the velocity fluctuation, which is evaluated with the aid of the hypothesis that fourth moments are related to second moments in the same way as for a normal joint distribution of the velocities at any two points. The experimental evidence relevant to this hypothesis (which cannot be exactly true since it gives zero odd-order moments) is examined. The alternative hypothesis made by Heisenberg, that the Fourier coefficients of the velocity distribution are statistically independent, has identical consequences for the fourth moments of the velocity, although it does not lead to such convenient results.

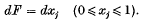
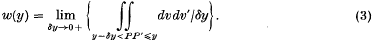
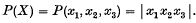
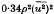The pressure correlation is worked out in detail for the important special case of very large Reynolds numbers of turbulence; the mean-square pressure fluctuation is found to be . The mean-square pressure gradient is evaluated, from the available data concerning the doublevelocity correlation, for the cases of very small and very large Reynolds numbers, and a simple interpolation between these results is suggested for the general case. Finally, the relation between the mean-square pressure gradient and rate of diffusion of marked fluid particles from a fixed source is established without the neglect of the viscosity effect, and the available observations of diffusion are used to obtain estimates of 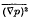which are compared with the theoretical values.

Recently an electromagnetic method for measuring the velocities of ocean currents for oceanographic purposes has been shown to be reliable enough for the observed velocity of the surface current to be taken into account in dead reckoning navigation in the open ocean. A preliminary test of the electromagnetic method as a navigational aid was made in 1949 on one cruise covering a distance of 1000 miles across the Gulf Stream and back. A total of 52 miles of lateral drift was corrected to produce a straight line of travel through the observed currents, and this correction enabled the ship to return to within 2 miles of the starting point. Seven less formal experiments performed in 1950 indicate that ordinarily, on straight-away courses, the lateral drift component caused by currents can be measured and corrected with the expectation that the undetected drift will be less than 1 percent of the distance travelled.

The position of a point on the surface will then be expressed by two spherical coordinates: namely, ist, the distance of the point from the primitive circle measured on a secondary; 2nd, the distance intercepted on the primitive circle between this secondary and some given point of the primitive circle assumed as the origin of coordinates.—William Chauvenet, Manual of Spherical and Practical Astronomy (1896).

On 16 May 1870, exactly eighty years before this paper was written, Lord Kelvin, then Sir William Thomson, worked out an epoch-making example of how to find the hour angle and azimuth of a heavenly body by inspection, in order to facilitate the use of Captain Thomas Sumner's method at sea. His work was published one year later in the Proceedings of the Royal Society, and in it he describes a page of his new Tables for Facilitating Sumner's Method at Sea. These tables, comprising nine pages, were made public on 11 November 1875 and were published in London in May of the following year; from them have been derived all modern navigation tables based on right-angled spherical triangles. Kelvin then used, for the first time, Greenwich hour angle in arc and assumed latitudes and longitudes. (The writer has himself used G.H.A. in arc since 1902 and assumed positions since 1908.)

The problem of evaluating the non-homogeneous critical determinant of the plane region |y − x2| ≤ 1 is solved as a particular case of a result concerning the non-homogeneous properties of convex regions proved in the author's thesis (not yet published). The search for an alternative method of proof led to a proof of the existence of an infinite sequence of minima analogous to the Markoff chain. This is the subject of the present paper.

The use of radar in relation to the Rule of the Road at sea is a subject over which there is still a great deal of controversy. An examination of the main problems involved was made in this Journal (Vol. 3, No. 1, January 1950) by Captain F. J. Wylie who concluded in his paper that the use of radar might justify a more liberal interpretation of the term ‘moderate speed’ than has hitherto been countenanced; and a recent amendment to the King's Regulations and Admiralty Instructions clearly accepts the use of radar as an existing circumstance within the meaning of Article 16.

No attempt, however, has so far been made to arrive at a precise definition of ‘moderate speed’, and it may well be that the reasons which prevented a definition being made in the non-radar case are in fact given more force when radar, with its added variables, is used. On the other hand it is unlikely that any progress in the matter can be made without a full discussion of the factors involved, and Captain Robb's paper, though it may be possible to dispute some of his conclusions, is presented here as an interesting attempt to achieve a definition which can serve as a guide to shipmasters.—Ed.

In a recent paper on shipborne radar the authors tried to analyze the mental approach of a master or pilot to the problem of handling his ship in a confined space when berthing in fog. The sense of loss that is caused by the absence of direct vision was referred to and various means by which confidence and control might be restored in these circumstances were considered. In that paper only the inadequacies of present-day shipborne radar in meeting these requirements were discussed. The approach to the problem can, however, be broadened to include the whole question of port operation in fog, and the present paper attempts to describe the general requirements and to consider in particular the role of shore-based radar and the manner in which the information obtained from radar or other aids should be presented to the master.

This paper is an appreciation of the navigational problems encountered during a flight round the world in 1948, in a single-engined light aircraft. The route chosen (Fig. 2) covered nearly every type of flying weather in the world, from the perfect conditions of the Mediterranean in the summer to the severe climate of the Aleutian islands; navigation tests were provided by the overwater flights across the South China Sea (Hong Kong—Okinawa = 900 miles), the North Pacific (Chitose—Shemya = 1730 miles) and the North Atlantic.

The Earth's magnetic field can evidently be divided into its horizontal and vertical components, the horizontal component being of more immediate interest to the navigator since it directs the compass needle in the horizontal plane. Whereas on the magnetic equator the full field is horizontal (about 0·400 c.g.s. units), in high latitudes, with the angle of dip between 60° and 70°, H, the horizontal force, maybe about 0·180 c.g.s. units. At the magnetic pole H is negligible and, given the opportunity, the compass needle would point vertically downwards, the instrument then having no directional properties in the horizontal plane.

Members will have learned with regret of the death of Dr. L. J. Comrie, M.A., PH.D., F.R.S., who died at the age of 57 on 11 December 1950. Dr. Comrie's contributions to science were primarily in the fields of astronomy and computation, and in the latter field he may be said to have created the modern concept of scientific computing and to have laid the foundations for the present widespread interest in numerical methods and in digital calculating machines. Tributes to this side of his work have already been paid, both here and abroad, and the Royal Society and the Royal Astronomical Society are both publishing fuller notices which will give a detailed assessment of his work. The following note, pays a tribute to Dr. Comrie's contribution to navigation.