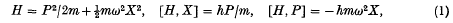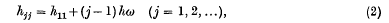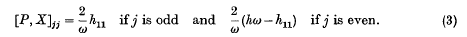Refine search
Actions for selected content:
26208 results in Theoretical Physics and Mathematical Physics
The Abridged Nautical Almanac
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, p. 316
- Print publication:
- July 1951
-
- Article
- Export citation
Humbert's plane sextics of genus 5
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 483-495
- Print publication:
- July 1951
-
- Article
- Export citation
The American Institute
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, p. 315
- Print publication:
- July 1951
-
- Article
- Export citation
Simplified Flight Planning
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 248-259
- Print publication:
- July 1951
-
- Article
- Export citation
On Boltzmann's equation in the kinetic theory of gases
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 602-609
- Print publication:
- July 1951
-
- Article
- Export citation
On the interaction between shock waves and boundary layers
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 545-553
- Print publication:
- July 1951
-
- Article
- Export citation
A New Decca Chain
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, p. 317
- Print publication:
- July 1951
-
- Article
- Export citation
A note on the correspondence between the x, t-plane and the characteristic plane in a problem of interaction of plane waves of finite amplitude
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 518-527
- Print publication:
- July 1951
-
- Article
- Export citation
The American Plan for Air Traffic Control: A Description of SC31
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 213-236
- Print publication:
- July 1951
-
- Article
- Export citation
The Australian Institute
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, p. 315
- Print publication:
- July 1951
-
- Article
- Export citation
NAV volume 4 issue 3 Back matter
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, p. b1
- Print publication:
- July 1951
-
- Article
-
- You have access
- Export citation
Qualifications for Fellowship
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 314-315
- Print publication:
- July 1951
-
- Article
- Export citation
On the use of convected coordinate systems in the mechanics of continuous media
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 575-584
- Print publication:
- July 1951
-
- Article
- Export citation
On a class of unirational varieties
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 496-503
- Print publication:
- July 1951
-
- Article
- Export citation
The finite-volume theorem for non-homogeneous lattices
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 627-628
- Print publication:
- July 1951
-
- Article
- Export citation
Ciro Caric's Tables
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, p. 325
- Print publication:
- July 1951
-
- Article
-
- You have access
- Export citation
On matrices whose eigenvalues are in arithmetic progression
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 585-590
- Print publication:
- July 1951
-
- Article
- Export citation
NAV volume 4 issue 3 Front matter
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. f1-f4
- Print publication:
- July 1951
-
- Article
-
- You have access
- Export citation
The surface energies of superconductors
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 617-625
- Print publication:
- July 1951
-
- Article
- Export citation
PSP volume 47 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- April 1951
-
- Article
-
- You have access
- Export citation