1. In this paper we consider the following problems, for continuous linear transformations in the space ω, whose points are arbitrary sequences of complex numbers, with the usual topology:

(a) the establishment of a spectral representation theorem; and

(b) the general description of the spectrum.

Oceanography is concerned with the applications of all sciences to the study of the sea, and navigation, in its widest sense, with the application of any science and systematic knowledge to the purpose of maintaining safe and efficient communications across the oceans. They have something in common, but oceanographical work, whatever its future promise, is primarily academic, and navigation the application of well-tried conclusions. It would be wrong to suggest that basic studies of sea conditions are followed by systematic attempts to use them to improve navigation. Progress is sporadic, depending on individual enthusiasms and commercial enterprise as well as the efforts of government departments and professional associations. There is no sharp division between the basic work and its applications, or, after allowing for some extremes, between the scientist and the authority on navigation.

1. Mazur(1) has shown that any normed algebra A over the real field in which the norm is multiplicative in the sense that

is equivalent (i.e. algebraically isomorphic and isometric under one and the same mapping) to one of the following algebras: (i) the real numbers, (ii) the complex numbers, (iii) the real quaternions, each of these sets being regarded as normed algebras over the real field. Completeness of A is not assumed by Mazur. A relevant discussion is given also in Lorch (2).

In the theory of beta-decay, as is well known, when the electron is described by relativistic wave-functions, e.g. in a Coulomb field, a difficulty arises when these become infinite at the centre of force, r = 0. The wave-functions are then evaluated at the nuclear radius, r = R, and in many formulae there appears (1) a rather sensitive dependence on R. For the capture of an orbital electron by a nucleus the results of calculation depend strongly on the behaviour of the wave-function of the bound electron near the nucleus. The nature of the potential energy near the nucleus will thus affect such quantities as the ratio of K-capture to positron emission. Wannier (2) has discussed a similar problem for the Schrödinger equation, but the singular behaviour of the solutions of the Dirac equation for the ground state makes it desirable to have the solution for the relativistic case. In the following, relativistic wave-functions are derived and used for a potential energy which is Coulombian outside the nucleus and constant inside. Similar problems have been considered by others, Breit et al. (3), Racah (4), in application to the calculation of hyperfine structure, and also by Broch (5).

On the asymptotic probability distribution for certain Markoff processes 46 (1950), 581.

By Walter Ledermann

Mr H. Schneider has drawn my attention to a mistake which occurs on p. 591 of the above paper.

The plan. During the spring and summer of 1950 three small British yachts sailed 15,000 miles in the open Atlantic, the object being to compete in the Bermuda race and then to race back across the Atlantic to Plymouth. Two of the craft, Cohoe and Samuel Pepys, were of under 5 tons displacement and the third, Mokoia, was very little bigger.

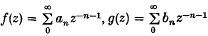When two functions are given, each with a finite radius of convergence, a theorem due independently to Hurwitz and Pincherle (1, 2) provides information about the position of the singularities of the function

in terms of the positions of the singularities of f(z) and g(z).

The close similarity between the basic problems in statistical thermodynamics and the partition theory of numbers is now well recognized. In either case one is concerned with partitioning a large integer, under certain restrictions, which in effect means that the ‘Zustandsumme’ of a thermodynamic assembly is identical with the generating function of partitions appropriate to that assembly. The thermodynamic approach to the partition problem is of considerable interest as it has led to generalizations which so far have not yielded to the methods of the analytic theory of numbers. An interesting example is provided in a recent paper of Agarwala and Auluck (1) where the Hardy Ramanujan formula for partitions into integral powers of integers is shown to be valid for non-integral powers as well.

The problems of submarine navigation are entirely distinct from those encountered on the surface. Not only does the medium introduce a third dimension, which is not wholly analagous to that of the air since a definite limit is imposed on depth, but also a great many of the aids to surface navigation are either restricted in their use underwater, or are wholly inappropriate and will not function. The use of the principal aids to submarine navigation is briefly described in this paper, future developments being mentioned where possible. A more detailed examination is then made of the problems of underwater navigation, problems in the main that affect the accuracy of keeping a reliable dead reckoning. An account is also given of a gravity survey carried out in H.M. Submarine Talent, during which the author served as navigating officer. On this operation the requirement for position accuracy was high, and some of the methods used were of considerable interest. The survey also provided the opportunity for current and tidal-stream observations to be made at different depths and an account of these observations is given.

Zygmund (1) proved in 1936 that if f(x) ∈Lp(−∞, ∞) (1 ≤ p ≤ 2), the Fourier transform

exists for almost every λ, in the sense that

exists for almost every λ. The purpose of this note is to provide a short proof of this theorem.