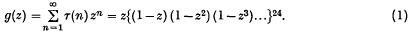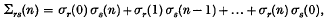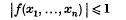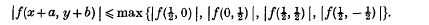Refine search
Actions for selected content:
26208 results in Theoretical Physics and Mathematical Physics
On the order of magnitude of Ramanujan's arithmetical function τ(n)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 4 / October 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 668-678
- Print publication:
- October 1951
-
- Article
- Export citation
Finite rotation groups and crystal classes in four dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 4 / October 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 650-661
- Print publication:
- October 1951
-
- Article
- Export citation
Parametric surfaces: I. Area
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 4 / October 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 687-698
- Print publication:
- October 1951
-
- Article
- Export citation
The Navigational Work of the C.S.I.R.O., Australia
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 4 / October 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 389-398
- Print publication:
- October 1951
-
- Article
- Export citation
Unification of the Air Almanac and the American Air Almanac
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 4 / October 1951
- Published online by Cambridge University Press:
- 01 October 1951, pp. 386-388
- Print publication:
- October 1951
-
- Article
- Export citation
On non-dissipative Markoff chains with an enumerable infinity of states
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 633-634
- Print publication:
- July 1951
-
- Article
- Export citation
Wave reflexion near a wall†
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 528-544
- Print publication:
- July 1951
-
- Article
- Export citation
The Construction of Hyperbolic Lattices
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 237-247
- Print publication:
- July 1951
-
- Article
- Export citation
On the law of decay of homogeneous isotropic turbulence and the theories of the equilibrium and similarity spectra
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 554-574
- Print publication:
- July 1951
-
- Article
- Export citation
A trigonometrical inequality
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 629-632
- Print publication:
- July 1951
-
- Article
- Export citation
Annual Awards
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, p. 314
- Print publication:
- July 1951
-
- Article
- Export citation
A Proposed Polar Navigation Table - Notes Techniques du Ministère de l'Air No. 35. ‘Le Point Astronomique Simplifié dans les Régions Polaires’. P. Hugon, viii + 16 pages, 7 × 10½ in., price 200 Fr.
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 320-321
- Print publication:
- July 1951
-
- Article
- Export citation
Plotting a Position Line Without Reference to an Azimuth
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 309-313
- Print publication:
- July 1951
-
- Article
- Export citation
New Astronomical Navigation Tables
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, p. 316
- Print publication:
- July 1951
-
- Article
- Export citation
Differential forms on a Kähler manifold
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 504-517
- Print publication:
- July 1951
-
- Article
- Export citation
Proposals for a New Air Navigation Chart
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, p. 323
- Print publication:
- July 1951
-
- Article
-
- You have access
- Export citation
Non-homogeneous binary cubic forms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 457-460
- Print publication:
- July 1951
-
- Article
- Export citation
PSP volume 47 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- July 1951
-
- Article
- Export citation
The Sensory Basis of Bird Navigation
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 260-275
- Print publication:
- July 1951
-
- Article
- Export citation
The Canadian Institute of Navigation
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 3 / July 1951
- Published online by Cambridge University Press:
- 18 January 2010, p. 316
- Print publication:
- July 1951
-
- Article
- Export citation