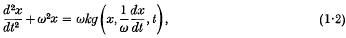Refine search
Actions for selected content:
26208 results in Theoretical Physics and Mathematical Physics
The stopping power of liquid water
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 443-449
- Print publication:
- April 1951
-
- Article
- Export citation
Thomas Gray Memorial Trust
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 18 January 2010, p. 208
- Print publication:
- April 1951
-
- Article
- Export citation
On a class of determinantal primals and their multiple loci
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 286-298
- Print publication:
- April 1951
-
- Article
- Export citation
Statistics of the simple cubic lattice
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 419-435
- Print publication:
- April 1951
-
- Article
- Export citation
Note on a penny-shaped crack under shear
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 396-400
- Print publication:
- April 1951
-
- Article
- Export citation
The thermodynamics of magnetization
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, p. 450
- Print publication:
- April 1951
-
- Article
-
- You have access
- Export citation
On the representation of rational sections of the Grassmannian of lines of five dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 305-308
- Print publication:
- April 1951
-
- Article
- Export citation
On the product of three non-homogeneous linear forms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 260-265
- Print publication:
- April 1951
-
- Article
- Export citation
The function
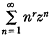 and associated polynomials
and associated polynomials
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 309-314
- Print publication:
- April 1951
-
- Article
- Export citation
Optimum Flight Paths
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 178-200
- Print publication:
- April 1951
-
- Article
- Export citation
NAV volume 4 issue 2 Front matter
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. f1-f4
- Print publication:
- April 1951
-
- Article
-
- You have access
- Export citation
The Marine Observer's Handbook, issued by the Meteorological Office (7th edition, June 1950), 122 + iv pp. , cloth 9·6 × 6 in., illustrated. H.M. Stationery Office, 8s. 6d.
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 18 January 2010, p. 210
- Print publication:
- April 1951
-
- Article
- Export citation
An application of local uniformization to the theory of divisors
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 279-285
- Print publication:
- April 1951
-
- Article
- Export citation
On the recurrent solutions of a class of non-linear differential equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 315-330
- Print publication:
- April 1951
-
- Article
- Export citation
The structure of the turbulent boundary layer
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 375-395
- Print publication:
- April 1951
-
- Article
- Export citation
Trapping modes in the theory of surface waves
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 347-358
- Print publication:
- April 1951
-
- Article
- Export citation
Notes on problems in hexagonal aeolotropic materials
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 401-409
- Print publication:
- April 1951
-
- Article
- Export citation
Quadrics in finite geometries
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 299-304
- Print publication:
- April 1951
-
- Article
- Export citation
A regression problem
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 337-346
- Print publication:
- April 1951
-
- Article
- Export citation
Curvilinear momenta in quantum mechanics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 451-453
- Print publication:
- April 1951
-
- Article
- Export citation
 of lines of
of lines of  by a general
by a general 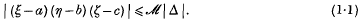
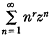 and associated polynomials
and associated polynomials
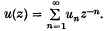
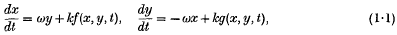
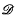 and are periodic in
and are periodic in