Refine search
Actions for selected content:
26208 results in Theoretical Physics and Mathematical Physics
High Altitude Observations at Sea
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 165-166
- Print publication:
- April 1951
-
- Article
- Export citation
I—Special Problems in Polar Regions
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 2 / April 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 126-135
- Print publication:
- April 1951
-
- Article
- Export citation
Circumventing the Dimness of the Radar Screen
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 106-107
- Print publication:
- January 1951
-
- Article
-
- You have access
- Export citation
Self-consistent field, with exchange, for Ne III
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 243-244
- Print publication:
- January 1951
-
- Article
- Export citation
A comparison of heisenberg's spectrum of turbulence with experiment
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 158-176
- Print publication:
- January 1951
-
- Article
- Export citation
The quadratic form positive definite on a linear manifold
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-6
- Print publication:
- January 1951
-
- Article
- Export citation
On the use of the characteristic functional in the analysis of some stochastic processes occurring in physics and biology
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 65-76
- Print publication:
- January 1951
-
- Article
- Export citation
The general motion of a sphere in a viscous liquid
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 142-145
- Print publication:
- January 1951
-
- Article
- Export citation
Upper Winds - Upper Winds over the World. C. E. P. Brooks, C. S. Durst, N. Carruthers, D. Dewar and J. S. Sawyer (Meteorological Office Geophysical Memoirs No. 85). H.M. Stationery Office, 1950, 149 pp., paper 11 × 8·5 in., 17s. 6d.
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 101-102
- Print publication:
- January 1951
-
- Article
- Export citation
On the propagation of disturbances from moving sources
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 109-126
- Print publication:
- January 1951
-
- Article
- Export citation
The Oldest Mediterranean Pilot
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 81-85
- Print publication:
- January 1951
-
- Article
- Export citation
Fourth Annual General Meeting
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 93-99
- Print publication:
- January 1951
-
- Article
- Export citation
Space-time on the rotating disk
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 177-189
- Print publication:
- January 1951
-
- Article
- Export citation
On the interaction of colloidal particles V. nature of repulsion between particles in dilute sols
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 230-242
- Print publication:
- January 1951
-
- Article
- Export citation
Diagrammatic Solutions for Astronomical Navigation
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 12-19
- Print publication:
- January 1951
-
- Article
- Export citation
On the interaction of colloidal particles IV. general mathematical theory for two identical particles
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 217-229
- Print publication:
- January 1951
-
- Article
- Export citation
Extensions and applications of a tauberian theorem due to valiron
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 22-37
- Print publication:
- January 1951
-
- Article
- Export citation
Equivalent Headwinds - Equivalent Headwinds. Compiled by J. S. Sawyer (Meteorological Report No. 6). H.M. Stationery Office, 1950, 20 pp., paper 9·6 × 6 in., 9d. - Equivalent Headwinds on Some Principal Air Routes of the World (Meteorological Report No. 7). H.M. Stationery Office, 1950, 16 + iv pp., paper 9·6 × 6 in., 9d.
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 102-104
- Print publication:
- January 1951
-
- Article
- Export citation
A problem on topological transformations of the plane. II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 47 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 24 October 2008, pp. 38-45
- Print publication:
- January 1951
-
- Article
- Export citation
Astro-fix by Ranges
-
- Journal:
- The Journal of Navigation / Volume 4 / Issue 1 / January 1951
- Published online by Cambridge University Press:
- 18 January 2010, pp. 20-30
- Print publication:
- January 1951
-
- Article
- Export citation
 of wave-length 3967 and
of wave-length 3967 and  of wave-length 3869 in the configuration Ne III 1
of wave-length 3869 in the configuration Ne III 1

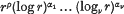 , where α
, where α