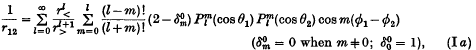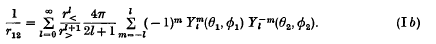Refine search
Actions for selected content:
26208 results in Theoretical Physics and Mathematical Physics
The Cambridge Philosophical Society Statement of Accounts for the Year Ending 31 July 1949
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 659-661
- Print publication:
- October 1950
-
- Article
- Export citation
On the expansion of a Coulomb potential in spherical harmonics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 626-633
- Print publication:
- October 1950
-
- Article
- Export citation
NAV volume 3 issue 4 Cover and Back matter
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. b1-b2
- Print publication:
- October 1950
-
- Article
- Export citation
The American Institute
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 425-426
- Print publication:
- October 1950
-
- Article
- Export citation
The distribution of the integers N for which {θN} < φ
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 525-534
- Print publication:
- October 1950
-
- Article
- Export citation
Sail Training for Navigation
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 431-432
- Print publication:
- October 1950
-
- Article
-
- You have access
- Export citation
The Reduction of Consol Bearings for Plotting
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 412-415
- Print publication:
- October 1950
-
- Article
- Export citation
Astro-Fix by Computation
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 430-431
- Print publication:
- October 1950
-
- Article
-
- You have access
- Export citation
Half-Convergency Corrections for Consol
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, p. 426
- Print publication:
- October 1950
-
- Article
- Export citation
Honorary Members and Fellows Elected
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 422-425
- Print publication:
- October 1950
-
- Article
- Export citation
The Use of Consol in the Fishing Fleet
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 347-349
- Print publication:
- October 1950
-
- Article
- Export citation
Navigational Awards
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, p. 425
- Print publication:
- October 1950
-
- Article
- Export citation
Conduction of heat in a solid with a power law of heat transfer at its surface
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 634-641
- Print publication:
- October 1950
-
- Article
- Export citation
The Australian Institute
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, p. 426
- Print publication:
- October 1950
-
- Article
- Export citation
The Air Accuracy of Compasses
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 404-411
- Print publication:
- October 1950
-
- Article
- Export citation
Electronic Navigation. Leonard M. Orman, Weems System of Navigation (Annapolis) and Pan American Navigation Service (Hollywood), 1950, 222, xiv, 1 plate, cloth 6·25 × 9·5 in. $4·50.
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 427-429
- Print publication:
- October 1950
-
- Article
- Export citation
Index
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 433-435
- Print publication:
- October 1950
-
- Article
- Export citation
I—The Dynamics of Space Flight
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 357-364
- Print publication:
- October 1950
-
- Article
- Export citation
An Instantaneous Fix on Two Bodies
-
- Journal:
- The Journal of Navigation / Volume 3 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 18 January 2010, pp. 389-392
- Print publication:
- October 1950
-
- Article
- Export citation
A theorem of Vinogradoff on uniform distribution
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 46 / Issue 4 / October 1950
- Published online by Cambridge University Press:
- 24 October 2008, pp. 642-644
- Print publication:
- October 1950
-
- Article
- Export citation